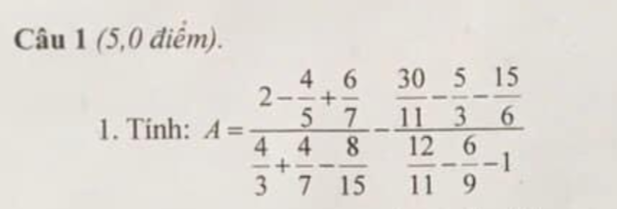Ta có:
\(A=\frac{1}{2.9}+\frac{1}{9.7}+\frac{1}{7.19}+...+\frac{1}{252.509}\)
\(A=\frac{2}{5}.\left(\frac{5}{4.9}+\frac{5}{9.14}+\frac{5}{14.19}+...+\frac{1}{504.509}\right)\)
\(A=\frac{2}{5}.\left(\frac{1}{4}-\frac{1}{9}+\frac{1}{9}-\frac{1}{14}+\frac{1}{14}-\frac{1}{19}+...+\frac{1}{504}-\frac{1}{509}\right)\)
\(A=\frac{2}{5}.\left(\frac{1}{4}-\frac{1}{509}\right)\)
\(A=\frac{2}{5}.\frac{505}{2036}\)
\(A=\frac{101}{1018}.\)
Vậy \(A=\frac{101}{1018}.\)
Chúc bạn học tốt!