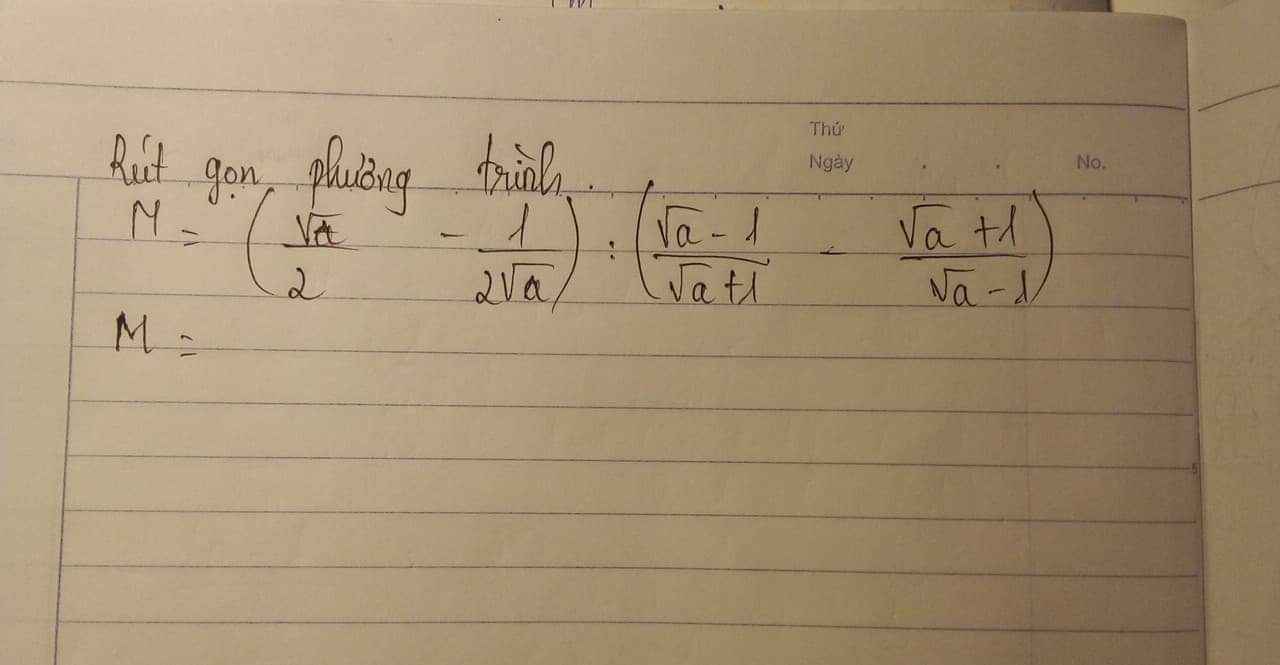ĐKXĐ : \(\left\{{}\begin{matrix}a>0\\a\ne1\end{matrix}\right.\)
Ta có :
\(M=\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right):\left(\dfrac{\sqrt{a}-1}{\sqrt{a}+1}-\dfrac{\sqrt{a}+1}{\sqrt{a}-1}\right)\)
\(=\left(\dfrac{a-1}{2\sqrt{a}}\right):\left(\dfrac{\left(\sqrt{a}-1\right)^2-\left(\sqrt{a}+1\right)^2}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\right)\)
\(=\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{2\sqrt{a}}.\dfrac{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}{\left(\sqrt{a}-1-\sqrt{a}-1\right)\left(\sqrt{a}-1+\sqrt{a}+1\right)}\)
\(=\dfrac{\left(\sqrt{a}-1\right)^2\left(\sqrt{a}+1\right)^2}{-8\sqrt{a}}\)
Vậy....