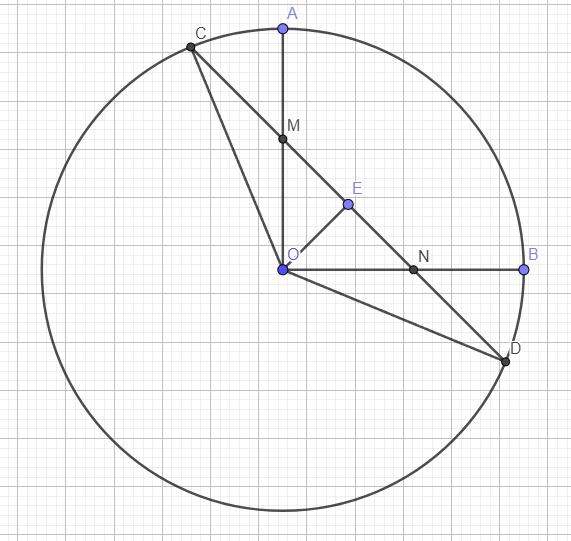
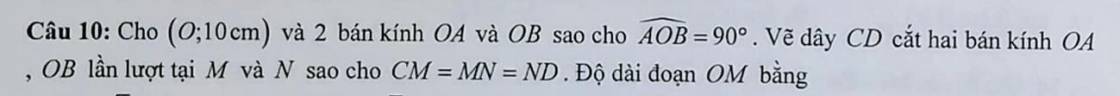Gọi E là trung điểm MN \(\Rightarrow ME=NE\Rightarrow CE=DE\) (do \(CM=DN\))
\(\Rightarrow E\) là trung điểm CD \(\Rightarrow OE\perp CD\) tại E
\(\Rightarrow\Delta OMN\) cân tại O (do OE là trung tuyến đồng thời là đường cao)
Đặt \(EM=EN=a\Rightarrow CM=DN=2a\) đồng thời \(OE=\dfrac{1}{2}MN=ME=a\) (trung tuyến ứng với cạnh huyền)
Pitago tam giác OEC: \(OE^2+CE^2=OC^2\)
\(\Leftrightarrow a^2+\left(2a+a\right)^2=10^2\Rightarrow a=\sqrt{10}\)
Pitago tam giác OEM: \(a^2+a^2=OM^2\Rightarrow OM=a\sqrt{2}=\sqrt{20}=2\sqrt{5}\)
Đúng 2
Bình luận (0)
