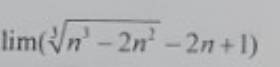\(lim\left(\sqrt[3]{n^3-2n^2}-2n+1\right)\)
\(=lim\dfrac{n^3-2n^2-\left(2n-1\right)^3}{\left(\sqrt[3]{n^3-2n^2}\right)^2+\sqrt[3]{n^3-2n^2}\left(2n-1\right)+\left(2n-1\right)^2}\)
\(=lim\dfrac{n^3-2n^2-\left(8n^3-12n^2+6n-1\right)}{\sqrt[3]{n^6-4n^5+4n^4}+\sqrt[3]{n^3-2n^2}\left(2n-1\right)+4n^2-4n+1}\)
\(=lim\dfrac{-7n^3+10n^2-6n+1}{\sqrt[3]{n^6-4n^5+4n^4}+\sqrt[3]{n^3-2n^2}\left(2n-1\right)+4n^2-4n+1}\)
\(=lim\dfrac{-7+\dfrac{10}{n}-\dfrac{6}{n^2}+\dfrac{1}{n^3}}{\sqrt[3]{\dfrac{1}{n^3}-\dfrac{4}{n^4}+\dfrac{4}{n^5}}+\sqrt[3]{\dfrac{1}{n^3}-\dfrac{2}{n^4}}\left(2-\dfrac{1}{n}\right)+\dfrac{4}{n}-\dfrac{4}{n^2}+\dfrac{1}{n^3}}\)
\(=\dfrac{-7}{0}=-\infty\)