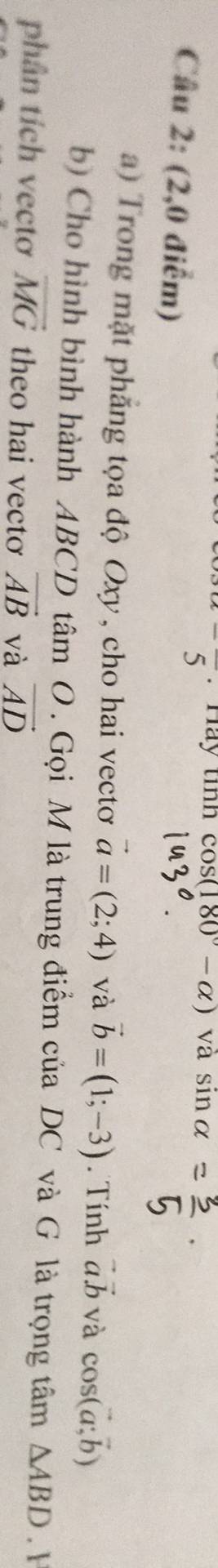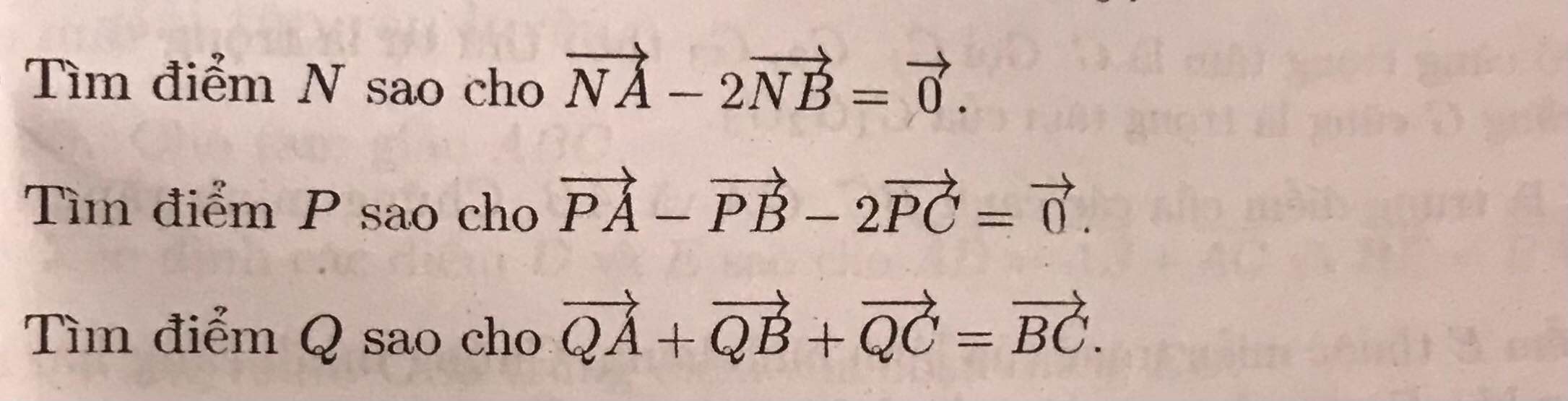b: Gọi giao điểm của BG với AD là K, E là giao điểm của DG với AB
Xét ΔABD có
G là trọng tâm
K là giao điểm của BG với AD
E là giao điểm của DG với AB
Do đó: K là trung điểm của AD và E là trung điểm của AB
Xét ΔABD có
G là trọng tâm của ΔABD
AO là đường trung tuyến
Do đó: \(AG=\dfrac{2}{3}\cdot AO=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot AC=\dfrac{1}{3}\cdot AC\)
AG+GC=AC
=>\(GC+\dfrac{1}{3}AC=AC\)
=>\(GC=\dfrac{2}{3}AC\)
Xét ΔDAB có
G là trọng tâm
DE là đường trung tuyến
Do đó; \(DG=\dfrac{2}{3}DE\)
Xét ΔGDC có GM là trung tuyến
nên \(\overrightarrow{GM}=\dfrac{1}{2}\left(\overrightarrow{GD}+\overrightarrow{GC}\right)\)
\(=\dfrac{1}{2}\left(-\dfrac{2}{3}\overrightarrow{DE}+\dfrac{2}{3}\cdot\overrightarrow{AC}\right)\)
\(=\dfrac{1}{3}\left(-\overrightarrow{DE}+\overrightarrow{AC}\right)\)
\(=\dfrac{1}{3}\left(-\dfrac{1}{2}\cdot\left(\overrightarrow{DA}+\overrightarrow{DB}\right)+\overrightarrow{AB}+\overrightarrow{AD}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{1}{2}\overrightarrow{AD}-\dfrac{1}{2}\overrightarrow{DB}+\overrightarrow{AB}+\overrightarrow{AD}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{3}{2}\overrightarrow{AD}-\dfrac{1}{2}\left(\overrightarrow{DA}+\overrightarrow{AB}\right)+\overrightarrow{AB}\right)\)
\(=\dfrac{1}{3}\left(\dfrac{3}{2}\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AD}-\dfrac{1}{2}\overrightarrow{AB}+\overrightarrow{AB}\right)\)
\(=\dfrac{1}{3}\left(2\overrightarrow{AD}+\dfrac{1}{2}\overrightarrow{AB}\right)\)
\(=\dfrac{2}{3}\overrightarrow{AD}+\dfrac{1}{6}\overrightarrow{AB}\)
a: \(\overrightarrow{a}=\left(2;4\right);\overrightarrow{b}=\left(1;-3\right)\)
=>\(\overrightarrow{a}\cdot\overrightarrow{b}=2\cdot1+4\cdot\left(-3\right)=-10\)
\(\left|\overrightarrow{a}\right|=\sqrt{2^2+4^2}=2\sqrt{10}\)
\(\left|\overrightarrow{b}\right|=\sqrt{1^2+\left(-3\right)^2}=\sqrt{10}\)
\(cos\left(\overrightarrow{a};\overrightarrow{b}\right)=\dfrac{\overrightarrow{a}\cdot\overrightarrow{b}}{\left|\overrightarrow{a}\right|\cdot\overrightarrow{b}}=\dfrac{-10}{2\sqrt{10}\cdot\sqrt{10}}=-\dfrac{1}{2}\)
=>\(\left(\overrightarrow{a};\overrightarrow{b}\right)=120^0\)