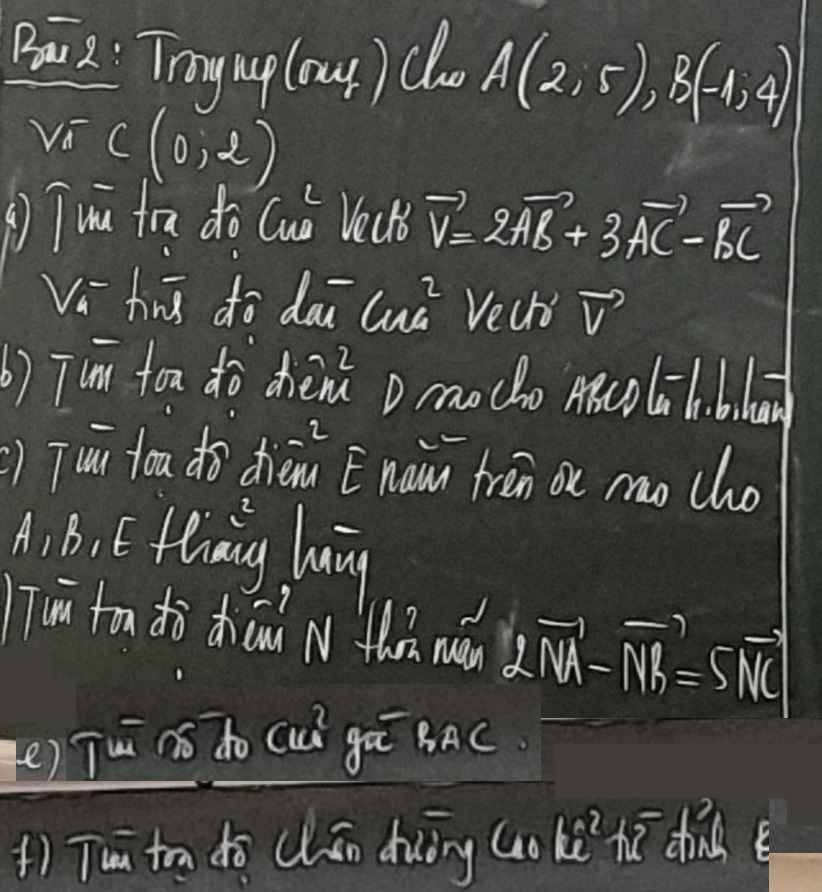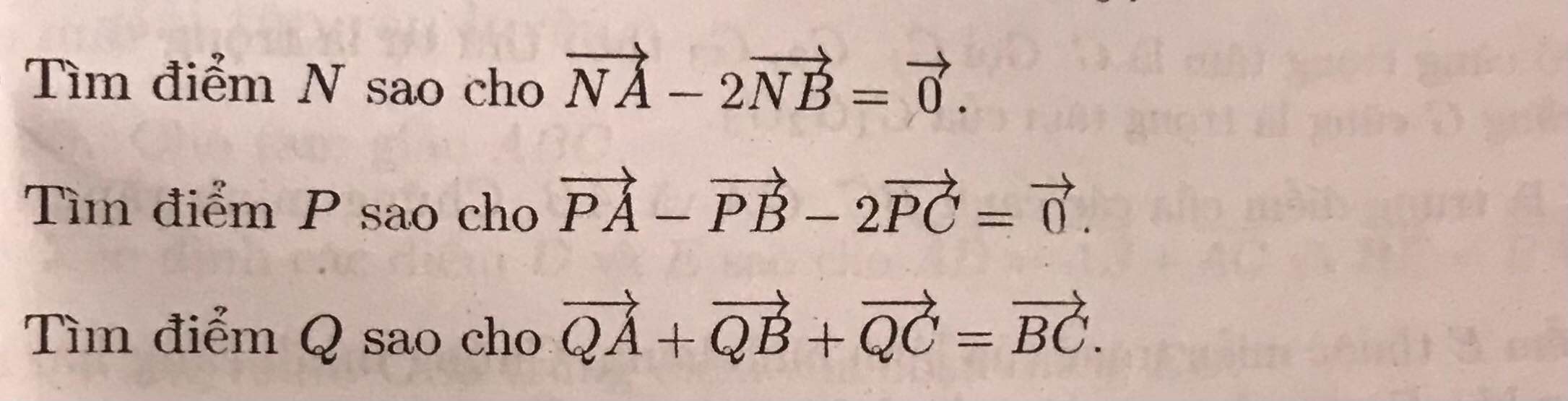a: A(2;5); B(-1;4); C(0;2)
Tọa độ vecto AB là:
\(\left\{{}\begin{matrix}x=-1-2=-3\\y=4-5=-1\end{matrix}\right.\)
Tọa độ vecto AC là:
\(\left\{{}\begin{matrix}x=0-2=-2\\y=2-5=-3\end{matrix}\right.\)
Tọa độ vecto BC là:
\(\left\{{}\begin{matrix}x=0-\left(-1\right)=1\\y=2-4=-2\end{matrix}\right.\)
Vậy: \(\overrightarrow{AB}=\left(-3;-1\right);\overrightarrow{AC}=\left(-2;-3\right);\overrightarrow{BC}=\left(1;-2\right)\)
\(\overrightarrow{V}=2\overrightarrow{AB}+3\overrightarrow{AC}-\overrightarrow{BC}\)
=>\(\overrightarrow{V}=\left(2\cdot\left(-3\right)+3\left(-2\right)-1;2\cdot\left(-1\right)+3\left(-3\right)-\left(-2\right)\right)\)
=>\(\overrightarrow{V}=\left(-13;-9\right)\)
\(\left|\overrightarrow{V}\right|=\sqrt{\left(-13\right)^2+\left(-9\right)^2}=\sqrt{198}=9\sqrt{22}\)
b: ABCD là hình bình hành
=>\(\overrightarrow{AB}=\overrightarrow{DC}\)
mà \(\overrightarrow{AB}=\left(-3;-1\right);\overrightarrow{DC}=\left(-x;2-y\right)\)
nên \(\left\{{}\begin{matrix}-x=-3\\2-y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=3\end{matrix}\right.\)
Vậy: D(3;3)
c: E nằm trên tia Ox nên E(x;0)
\(\overrightarrow{AB}=\left(-3;-1\right);\overrightarrow{AE}=\left(x-2;-5\right)\)
A,B,E thẳng hàng nên \(\dfrac{x-2}{-3}=\dfrac{-5}{-1}=5\)
=>x-2=-15
=>x=-15+2=-13
vậy: E(-13;0)
d: \(\overrightarrow{NA}=\left(2-x;5-y\right);\overrightarrow{NB}=\left(-1-x;4-y\right);\overrightarrow{NC}=\left(-x;2-y\right)\)
\(2\overrightarrow{NA}-\overrightarrow{NB}=5\overrightarrow{NC}\)
=>\(\left\{{}\begin{matrix}2\left(2-x\right)-\left(-1-x\right)=5\left(-x\right)\\2\left(5-y\right)-\left(4-y\right)=5\left(2-y\right)\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4-2x+x+1=-5x\\10-2y-4+y=10-5y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-5x=-x+5\\-5y+10=-y+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-4x=5\\-4y=-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{5}{4}\\y=1\end{matrix}\right.\)
Vậy: \(N\left(-\dfrac{5}{4};1\right)\)
e: \(AB=\sqrt{\left(-3\right)^2+\left(-1\right)^2}=\sqrt{10}\)
\(AC=\sqrt{\left(-2\right)^2+\left(-3\right)^2}=\sqrt{13}\)
\(BC=\sqrt{1^2+\left(-2\right)^2}=\sqrt{5}\)
Xét ΔABC có \(cosBAC=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}=\dfrac{10+13-5}{2\cdot\sqrt{10}\cdot\sqrt{13}}\)
\(=\dfrac{18}{2\sqrt{130}}=\dfrac{9}{\sqrt{130}}\)
=>\(sinBAC=\sqrt{1-\left(\dfrac{9}{\sqrt{130}}\right)^2}=\dfrac{7}{\sqrt{130}}\)