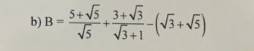Question

 

Answer 1

\(B=\dfrac{5+\sqrt{5}}{\sqrt{5}}+\dfrac{3+\sqrt{3}}{\sqrt{3}+1}-\left(\sqrt{3}+\sqrt{5}\right)\)

\(=\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}}+\dfrac{\sqrt{3}\left(\sqrt{3}+1\right)}{\sqrt{3}+1}-\sqrt{3}-\sqrt{5}\)

\(=\sqrt{5}+1+\sqrt{3}-\sqrt{3}-\sqrt{5}\)

=1

Answer 2

\(B=\dfrac{5+\sqrt{5}}{\sqrt{5}}+\dfrac{3+\sqrt{3}}{\sqrt{3}+1}-\left(\sqrt{3}+\sqrt{5}\right)\\ =\dfrac{\sqrt{5}\left(\sqrt{5}+1\right)}{\sqrt{5}}+\dfrac{\sqrt{3}\left(\sqrt{3}+1\right)}{\sqrt{3}+1}-\left(\sqrt{3}+\sqrt{5}\right)\\ =\sqrt{5}+1+\sqrt{3}-\sqrt{3}-\sqrt{5}\\ =1\)