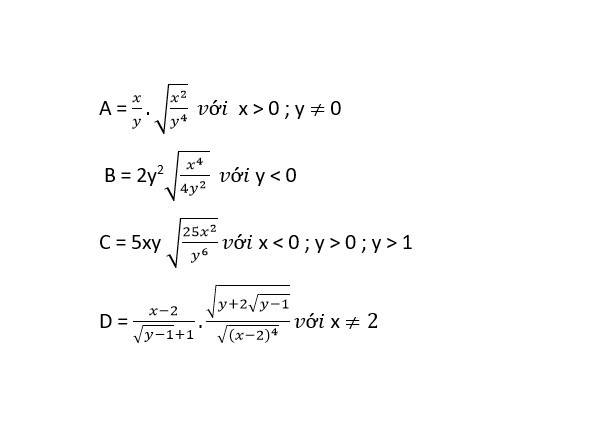a) \(A=\dfrac{x}{y}.\sqrt[]{\dfrac{x^2}{y^4}}\) \(\left(x>0;y\ne0\right)\)
\(\Leftrightarrow A=\dfrac{x}{y}.\sqrt[]{\left(\dfrac{x^{ }}{y^2}\right)^2}\)
\(\Leftrightarrow A=\dfrac{x}{y}.\left|\dfrac{x}{y^2}\right|\)
\(\Leftrightarrow A=\dfrac{x}{y}.\dfrac{x}{y^2}=\dfrac{x^2}{y^3}\left(x>0\right)\)
b) \(B=2y^2\sqrt[]{\dfrac{x^4}{4y^2}}\left(y< 0\right)\)
\(\Leftrightarrow B=2y^2\sqrt[]{\left(\dfrac{x^2}{2y^{ }}\right)^2}\)
\(\Leftrightarrow B=2y^2.\left|\dfrac{x^2}{2y^{ }}\right|\)
\(\Leftrightarrow B=2y^2.\dfrac{x^2}{-2y^{ }}\)
\(\Leftrightarrow B=-x^2y^{ }\)
c) \(C=5xy.\sqrt[]{\dfrac{25x^2}{y^6}}\left(x< 0;y>0;y>1\right)\)
\(\Leftrightarrow C=5xy.\sqrt[]{\left(\dfrac{5x^{ }}{y^3}\right)^2}\)
\(\Leftrightarrow C=5xy.\left|\dfrac{5x^{ }}{y^3}\right|\)
\(\Leftrightarrow C=5xy.\dfrac{-5x^{ }}{y^3}\)
\(\Leftrightarrow C=\dfrac{-25x^2}{y^2}\)
d) \(D=\dfrac{x-2}{\sqrt[]{y-1}+1}.\dfrac{\sqrt[]{y+2\sqrt[]{y-1}}}{\sqrt[]{\left(x-2\right)^4}}\left(x\ne2\right)\)
\(\Leftrightarrow D=\dfrac{x-2}{\sqrt[]{y-1}+1}.\dfrac{\sqrt[]{y-1+2\sqrt[]{y-1}+1}}{\left|\left(x-2\right)^2\right|}\)
\(\Leftrightarrow D=\dfrac{x-2}{\sqrt[]{y-1}+1}.\dfrac{\sqrt[]{\left(\sqrt[]{y-1}+1\right)^2}}{\left(x-2\right)^2}\)
\(\Leftrightarrow D=\dfrac{1}{\left(\sqrt[]{y-1}+1\right)}.\dfrac{\left|\sqrt[]{y-1}+1\right|}{x-2}\)
\(\Leftrightarrow D=\dfrac{1}{\left(\sqrt[]{y-1}+1\right)}.\dfrac{\sqrt[]{y-1}+1}{x-2}\)
\(\Leftrightarrow D=\dfrac{1}{x-2}\left(y\ge1;\sqrt[]{y-1}+1>0\right)\)