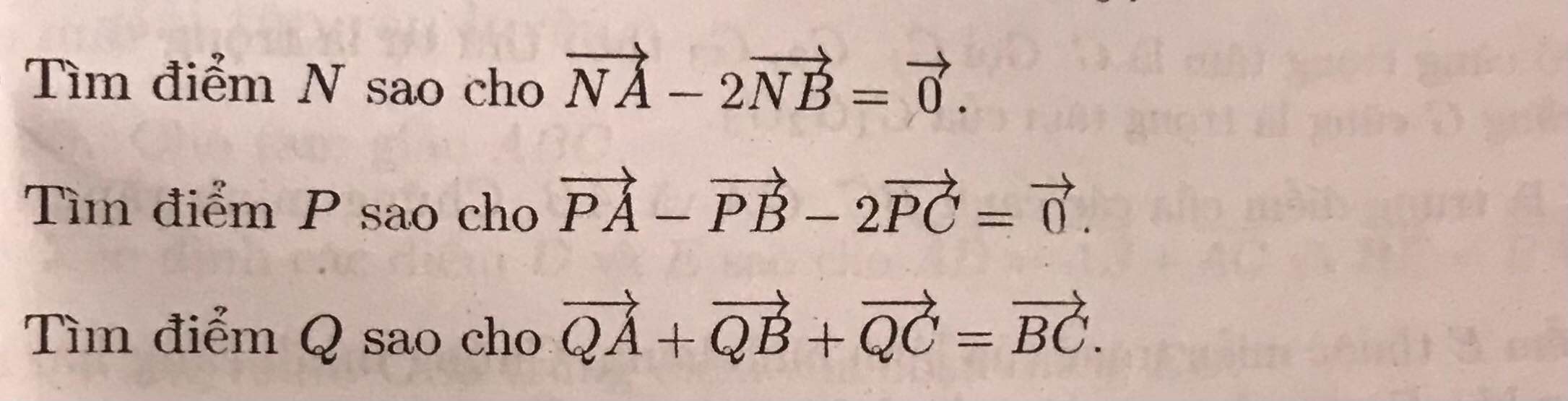\(A\left(4\sqrt[]{3};-1\right);B\left(0;3\right);C\left(8\sqrt[]{3};3\right)\)
a) Gọi \(D\left(x;y\right)\)
Để ABCD là hình bình hành
\(\Leftrightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\overrightarrow{DC}\\\overrightarrow{AD}=\overrightarrow{BC}\end{matrix}\right.\left(1\right)\)
mà \(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-4\sqrt[]{3};4\right)\\\overrightarrow{DC}=\left(8\sqrt[]{3}-x;3-y\right)\\\overrightarrow{AD}=\left(x-4\sqrt[]{3};y+1\right)\\\overrightarrow{BC}=\left(8\sqrt[]{3};0\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x-8\sqrt[]{3}}{4\sqrt[]{3}}=\dfrac{3-y}{4}\\\dfrac{x-4\sqrt[]{3}}{8\sqrt[]{3}}=\dfrac{y+1}{0}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x=44\sqrt[]{3}-4\sqrt[]{3}.y\\8\sqrt[]{3}\left(y+1\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=11\sqrt[]{3}-\sqrt[]{3}.\left(-1\right)=12\sqrt[]{3}\\y=-1\end{matrix}\right.\)
\(\Rightarrow D\left(12\sqrt[]{3};-1\right)\)
b) \(\overrightarrow{AD}=\left(8\sqrt[]{3};0\right)\)
\(\overrightarrow{AD}.\overrightarrow{AB}=\left(-96;0\right)\)
\(\overrightarrow{AD}.\overrightarrow{BC}=\left(192;0\right)\)