Question

Answer 1

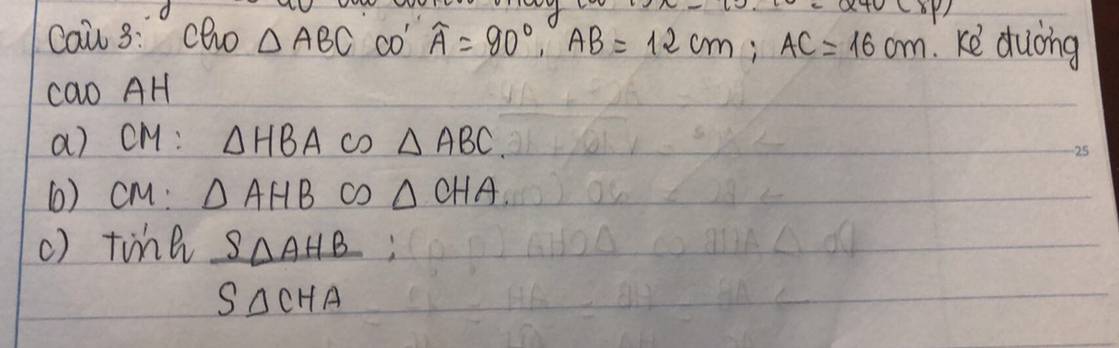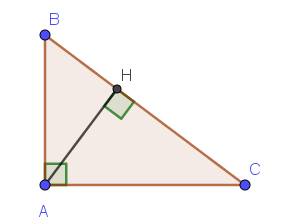
a) Xét hai tam giác vuông: \(\Delta HBA\) và  có:

\(\widehat{B}\) chung

\(\Rightarrow\Delta HBA\sim\Delta ABC\left(g-g\right)\)

b) Xét hai tam giác vuông: \(\Delta AHB\) và \(\Delta CHA\) có:

\(\widehat{HAB}=\widehat{HCA}\) (cùng phụ \(\widehat{B}\))

\(\Rightarrow\Delta AHB\sim\Delta CHA\left(g-g\right)\)

c) Do \(\Delta AHB\sim\Delta CHA\left(cmt\right)\)

\(\Rightarrow\) Tỉ số đồng dạng \(k=\dfrac{AB}{AC}=\dfrac{12}{16}=\dfrac{3}{4}\)

\(\Rightarrow\dfrac{S_{\Delta AHB}}{S_{\Delta CHA}}=k^2=\left(\dfrac{3}{4}\right)^2=\dfrac{9}{16}\)