Question

Answer 1

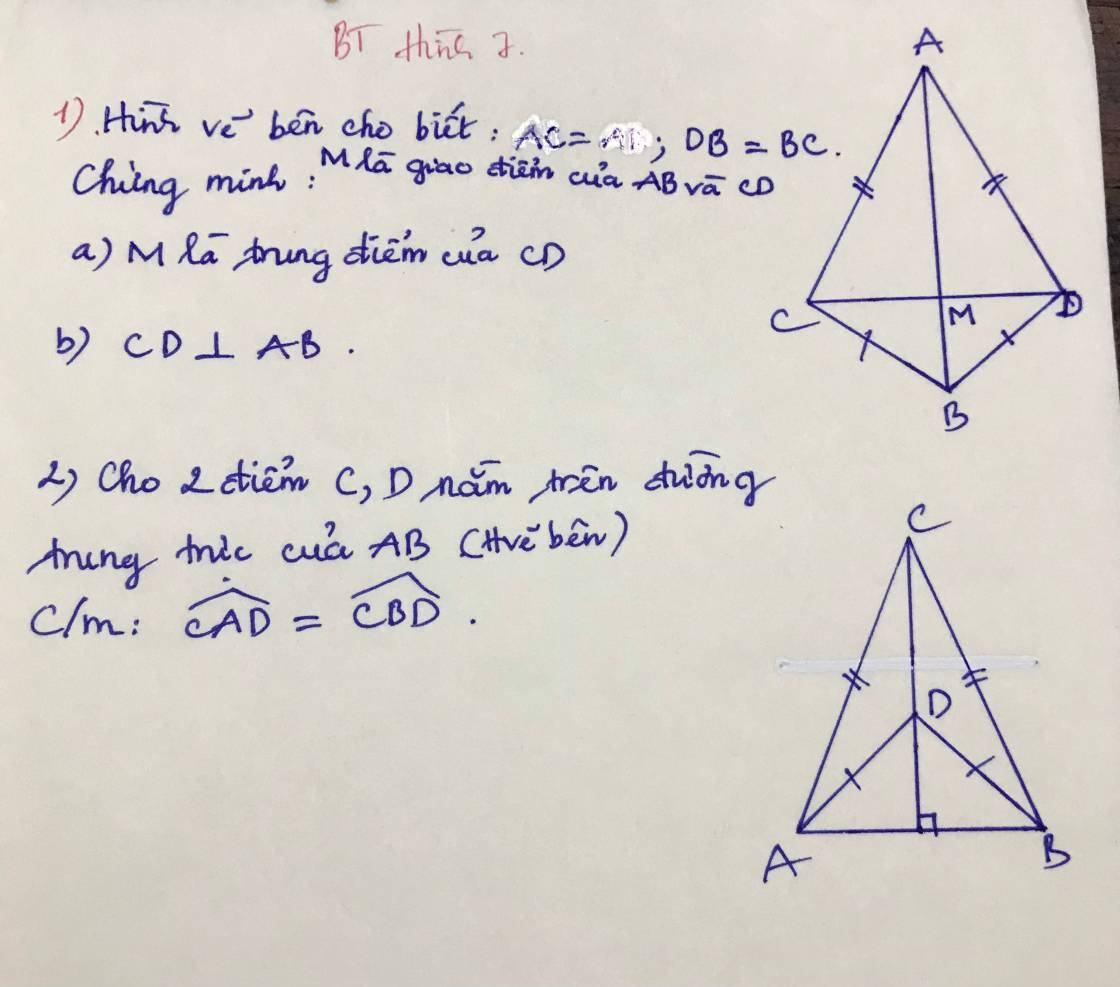
`1)`

`a,` Xét Tam giác `BAC` và Tam giác `BAD` có:

`AC = AD (g``t)`

`\text {AB chung}`

`BC = BD (g``t)`

`=> \text {Tam giác BAC = Tam giác BAD (c-c-c)}`

`->`\(\widehat{BAC}=\widehat{BAD} (\text {2 góc tương ứng})\)

Xét Tam giác `MAC` và Tam giác `MAD` có:

`AC = AD (g``t)`

\(\widehat{BAC}=\widehat{BAD} (CMT)\)

`\text {AM chung}`

`=> \text {Tam giác MAC = Tam giác MAD (c-g-c)}`

`-> MC = MB (\text {2 cạnh tương ứng})`

`-> \text {M là trung điểm của CD}.`

`b,` Vì Tam giác `MAC =` Tam giác `MAD (a)`

`->`\(\widehat{AMC}=\widehat{AMD} (\text {2 góc tương ứng})\)

Mà `2` góc này nằm ở vị trí kề bù

`->`\(\widehat{AMC}+\widehat{AMD}=180^0\)

`->`\(\widehat{AMC}=\widehat{AMD}=\) `180/2=90^0`

`-> CD \bot AB (đpcm).`

`2)`

Vì điểm `C, D` nằm trên đường trung trực của `AB`

Theo tính chất của đường trung trực

`-> AC = BC, DA = DB.`

Xét Tam giác `CAD` và Tam giác `CBD` có:

`AC = BC (CMT)`

`\text {CD chung}`

`DA = DB (CMT)`

`=> \text {Tam giác CAD = Tam giác CBD (c-c-c)}`

`->`\(\widehat{CAD}=\widehat{CBD} (\text {2 góc tương ứng}).\)