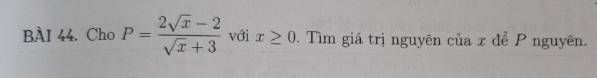ĐKXĐ: \(\sqrt{x}+3\ge0\Leftrightarrow x\ge\)
Ta có: \(P=\dfrac{2\sqrt{x}-2}{\sqrt{x}+3}=\dfrac{2\sqrt{x}+6-8}{\sqrt{x}+3}=\dfrac{2\left(\sqrt{x}+3\right)}{\sqrt{x}+3}-\dfrac{8}{\sqrt{x}+3}=2-\dfrac{8}{\sqrt{x}+3}\)
Để P có giá trị nguyên thì \(\dfrac{8}{\sqrt{x}+3}\) cũng nguyên
Do đó: \(\sqrt{x}+3\inƯ\left(8\right)\)
Mà \(Ư\left(8\right)=\left\{\pm1;\pm2;\pm4;\pm8\right\}\)
Bảng biện luận
| \(\sqrt{x}+3\) | \(-1\) | \(1\) | \(-2\) | \(2\) | \(-4\) | \(4\) | \(-8\) | \(8\) |
| \(x\) | loại | loại | loại | loại | loại | \(1\) | loại | \(25\) |
Vậy khi \(x=1\) hoặc \(x=25\) để P nguyên
Đúng 1
Bình luận (0)
