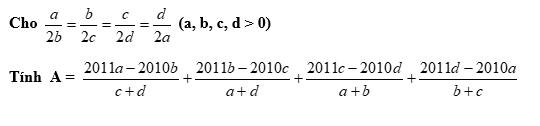Question

Answer 1

Ta có: \(\frac{a}{2b}=\frac{b}{2c}=\frac{c}{2d}=\frac{d}{2a}\)

=>\(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=\frac{d}{a}\)

Đặt \(\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=\frac{d}{a}=k\) (Điều kiện: k>0)

=>\(d=ak;c=dk;b=ck;a=bk\)

=>d=ak; \(c=ak\cdot k=ak^2\) ; \(b=ak^2\cdot k=ak^3\) ; \(a=ak^3\cdot k=a\cdot k^4\)

=>\(k^4=1\)

=>k=1

=>d=a=b=c

\(A=\frac{2011a-2010b}{c+d}+\frac{2011b-2010c}{a+d}+\frac{2011c-2010d}{a+b}+\frac{2011d-2010a}{b+c}\)

\(=\frac{2011a-2010a}{a+a}+\frac{2011a-2010a}{a+a}+\frac{2011a-2010a}{a+a}+\frac{2011a-2010a}{a+a}\)

\(=\frac12+\frac12+\frac12+\frac12=2\)