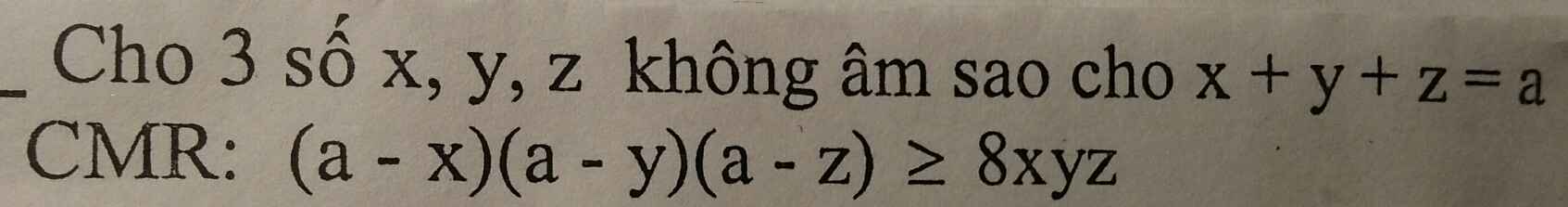Ta chứng minh BĐT sau với các số không âm:
\(x+y\ge2\sqrt{xy}\)
Thật vậy, BĐT tương đương: \(\left(\sqrt{x}-\sqrt{y}\right)^2\ge0\) (luôn đúng)
Lại có
\(\left\{{}\begin{matrix}a-x=x+y+z-x=y+z\\a-y=x+z\\a-z=x+y\end{matrix}\right.\)
Do đó:
\(VT=\left(y+z\right)\left(x+z\right)\left(x+y\right)\ge2\sqrt{yz}.2\sqrt{xz}.2\sqrt{xy}=8xyz\) (đpcm)
Dấu "=" xảy ra khi \(x=y=z=\dfrac{a}{3}\)
chứng minh với các bất đẳng thức sau bằng cách xét từng khoảng giá trị của biến
a)A =\(x^4+x^3+x^2+x+1>0\)
b)\(C=x^8-x^7+x^4-x+1>0\)
Giải các phương trình:
a) 1 - 2x = 2 - 3x
b) \(\frac{3x+2}{2}\) - \(\frac{3x+1}{6}\) =\(\frac{5}{3}\) +2x
c) \(\frac{2x-1}{5}\) - \(\frac{x-2}{3}\) = \(\frac{x+7}{15}\)
Cho ba số dương a,b,c thỏa mãn abc=1. Chứng minh rằng
\(\frac{1}{a^2+2b+3}+\frac{1}{b^2+2c+3}+\frac{1}{c^2+2a+3}\le\frac{1}{2}\)
Tìm các cặp số (x,y) thỏa mãn 3x2+y2+2x-2y=1
Câu 1: Một ô tô đi từ A đến B với vận tốc 40km/h, đến B ô tô nghỉ 1 giờ để dở hàng, rồi quay trở về A với vận tốc 60km/h, thời gian cả đi lẫn về ( kể cả thời gian nghỉ ở B ) là 5 giờ 30 phút. Tính quảng đường AB?
Câu 2: Cho góc nhọn xOy, trên tia Ox lấy hai điểm D và A sao cho OD = 3cm, OA = 8cm; trên tia Oy lấy hai điểm B và C sao cho OB = 4cm, OC= 6cm.
a) Chứng minh tam giác OAB đồng dạng với tam giác OCD.
b) Gọi M là giao điểm của AB và CD, chứng minh MA.MB = MC.MD.
c) Cho biết tổng chu vi của tam giác OAB và tam giác OCD là 38,5cm. Tính độ dài các đoạn thẳng AB và CD?
Câu 3: Giải phương trình | 14 - 3x | - 2x = 2x + 7.
Mấy bạn giúp mình giải gấp với. Chiều mai mình kiểm tra rồi ạ!
giải pt sau \(\left(\dfrac{x+1}{x-2}\right)^2-3\left(\dfrac{2x-4}{x-4}\right)^2+\dfrac{x+1}{x-4}=0\)
\(\frac{3}{2x-16}+\frac{3x-20}{x-8}+\frac{1}{8}=\frac{13x-102}{3x-24}\)
CHO CÁC SỐ a,b thỏa mãn \(4a^2+a=8b^2+b\).CHỨNG MINH RẰNG :a-b là số chính phương
Tìm giá trị lớn nhất hoặc nhỏ nhất của biểu thức:
a) x^2+x+1
b) 2+x-x^2
c) x^2-4x+1
d) 4x^2+4x+11
e) 3x^2-6x+1
f) x^2-2x+y^2-4y+6
cho a+b+c = 1 và a\(^3\) và a\(^3\)+b\(^3\)+c\(^3\) = 1
CMR: a\(^5\)+b\(^5\)+c\(^5\) = 1
