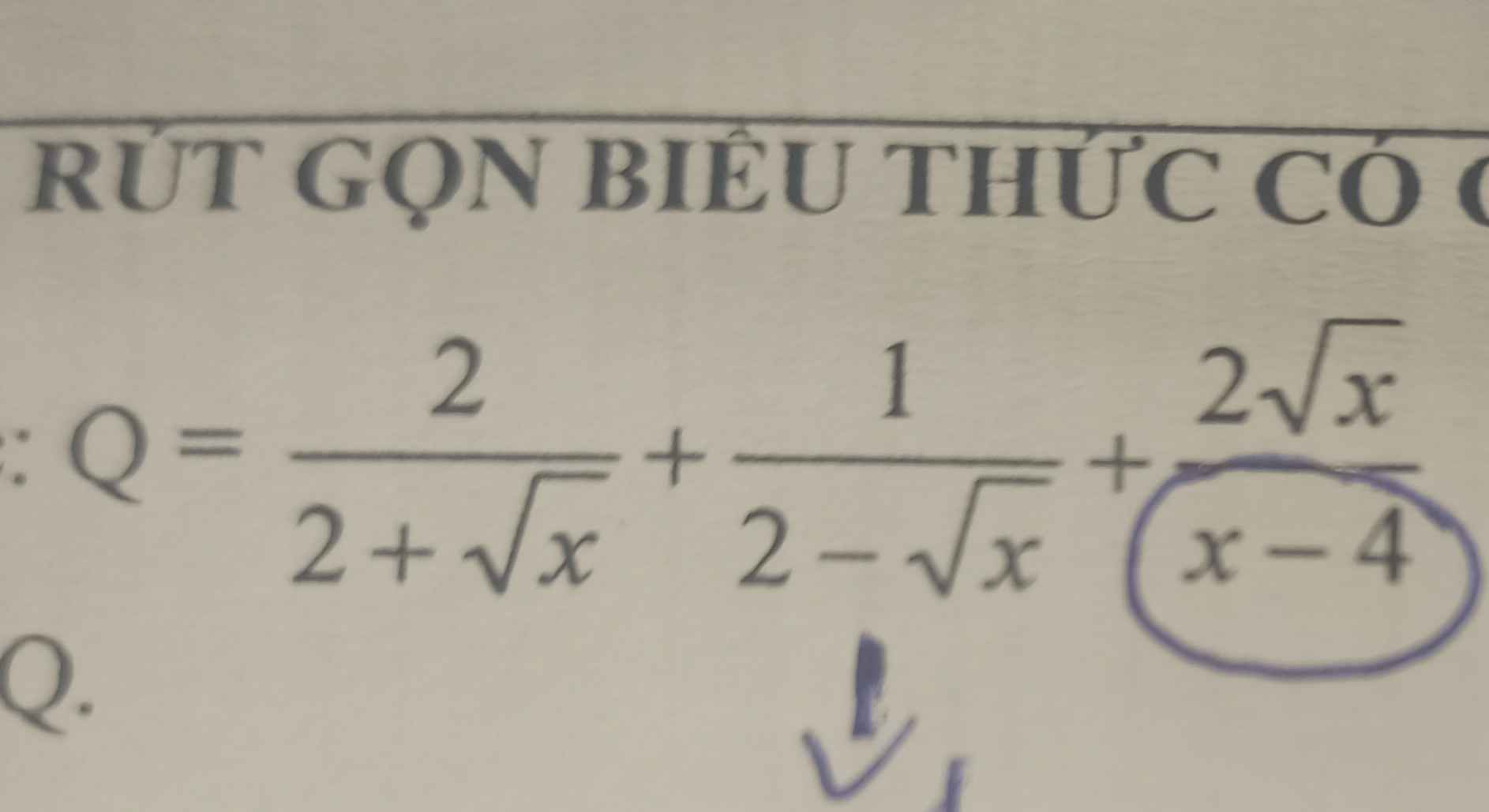\(=\dfrac{2\left(\sqrt{x}-2\right)-\left(\sqrt{x}+2\right)+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2\sqrt{x}-4-\sqrt{x}-2+2\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{3\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3}{\sqrt{x}+2}\)
\(Q=\dfrac{2}{2+\sqrt{x}}+\dfrac{1}{2-\sqrt{x}}+\dfrac{2\sqrt{x}}{x-4}\left(x\ge0;x\ne4\right)\)
\(=\dfrac{2\left(2-\sqrt{x}\right)}{4-x}+\dfrac{2+\sqrt{x}}{4-x}-\dfrac{2\sqrt{x}}{4-x}\)
\(=\dfrac{4-2\sqrt{x}+2+\sqrt{x}-2\sqrt{x}}{4-x}\)
\(=\dfrac{6-3\sqrt{x}}{4-x}\)
\(=\dfrac{3\left(2-\sqrt{x}\right)}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}\)
\(=\dfrac{3}{\sqrt{x}+2}\)
\(ĐKXĐ:x\ge0,x\ne4\)
\(Q=\dfrac{2}{2+\sqrt{x}}+\dfrac{1}{2-\sqrt{x}}+\dfrac{2\sqrt{x}}{x-4}\)
\(=\dfrac{2\left(2-\sqrt{x}\right)}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}+\dfrac{2+\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}-\dfrac{2\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}\)
\(=\dfrac{4-2\sqrt{x}+2+\sqrt{x}-2\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}\)
\(=\dfrac{6-3\sqrt{x}}{\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}\)
\(=\dfrac{3\left(2-\sqrt{x}\right)}{\text{}\left(2+\sqrt{x}\right)\left(2-\sqrt{x}\right)}=\dfrac{3}{\sqrt{x}+2}\)