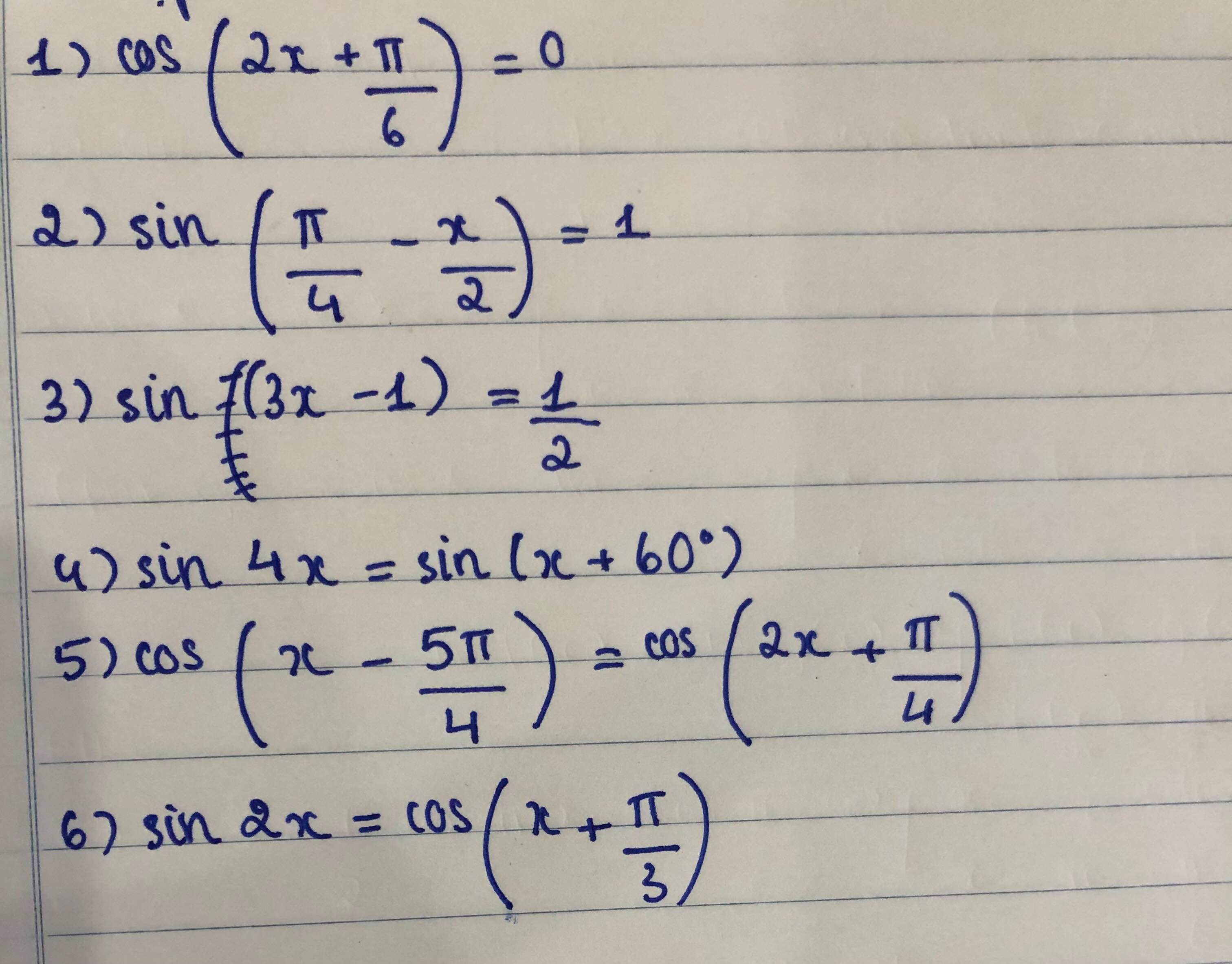\(1,cos\left(2x+\dfrac{\pi}{6}\right)=0.\\ \Leftrightarrow2x+\dfrac{\pi}{6}=k\pi.\\ \Leftrightarrow x=\dfrac{-\pi}{12}+k\dfrac{\pi}{2},k\in Z.\)
\(2,sin\left(\dfrac{\pi}{4}-\dfrac{x}{2}\right)=1.\\ \Leftrightarrow\dfrac{\pi}{4}-\dfrac{x}{2}=\dfrac{\pi}{2}+k2\pi.\\ \Leftrightarrow-\dfrac{x}{2}=\dfrac{\pi}{4}+k2\pi.\\ \Leftrightarrow x=\dfrac{-\pi}{2}-k\pi,k\in Z.\)
\(3,sin\left(3x-1\right)=\dfrac{1}{2}.\\ \Leftrightarrow sin\left(3x-1\right)=sin\dfrac{\pi}{6}.\\ \Leftrightarrow\left[{}\begin{matrix}3x-1=\dfrac{\pi}{6}+k2\pi.\\3x-1=\pi-\dfrac{\pi}{6}+k2\pi.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=\dfrac{\pi}{6}+1+k2\pi.\\3x=\dfrac{5}{6}\pi+1+k2\pi.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{18}+\dfrac{1}{3}+k\dfrac{2}{3}\pi.\\x=\dfrac{5}{18}\pi+\dfrac{1}{3}+k\dfrac{2}{3}\pi.\end{matrix}\right.\) \(\left(k\in Z\right).\)
\(4,sin4x=sin\left(x+60^o\right).\\ \Leftrightarrow sin4x=sin\left(x+\dfrac{\pi}{3}\right).\Leftrightarrow\left[{}\begin{matrix}4x=x+\dfrac{\pi}{3}+k2\pi.\\4x=\pi-x-\dfrac{\pi}{3}+k2\pi.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{9}+k\dfrac{2}{3}\pi.\\x=\dfrac{2}{15}\pi+k\dfrac{2}{5}\pi.\end{matrix}\right.\) \(\left(k\in Z\right).\)
\(5,cos\left(x-\dfrac{5\text{}\pi}{4}\right)=cos\left(2x+\text{}\dfrac{\pi}{4}\right).\\ \Leftrightarrow\left[{}\begin{matrix}x-\dfrac{5\text{}\pi}{4}=2x+\text{}\dfrac{\pi}{4}+k2\pi.\\x-\dfrac{5\text{}\pi}{4}=-2x-\text{}\dfrac{\pi}{4}+k2\pi.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\pi-k2\pi.\\x=\dfrac{\pi}{3}+k\dfrac{2\pi}{3}\end{matrix}\right.\) \(\left(k\in Z\right).\)
\(6,sin2x=cos\left(x+\text{}\dfrac{\text{}\pi}{3}\right).\\ sin2x=sin\left(\dfrac{\pi}{6}-x\right).\\ \Leftrightarrow\left[{}\begin{matrix}2x=\text{}\text{}\dfrac{\pi}{6}-x+k2\pi.\\2x=\pi-\dfrac{\pi}{6}+x+k2\pi.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{18}+k\dfrac{2}{3}\pi.\\x=\dfrac{5}{6}\pi+k2\pi.\end{matrix}\right.\)\(\left(k\in Z\right).\)