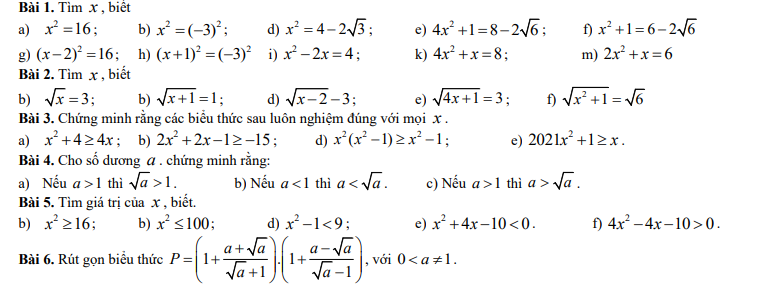\(a,x^2=16\\ \Rightarrow x^2=4^2\\ \Rightarrow x=4\\ b,x^2=\left(-3\right)^2\\ \Rightarrow x=-3\\ g,\left(x-2\right)^2=16\\ \Rightarrow\left(x-2\right)^2=4^2\\ \Rightarrow x-2=4\\ \Rightarrow x=2\\ h,\left(x+1\right)^2=\left(-3\right)^2\\ \Rightarrow x+1=-3\\ x=-3-1\\ x=-4\\ i,x^2-2x=4\\ \Rightarrow x^2-2x-4=0\\ \Delta'=b'^2-ac=\left(-1\right)^2-1\cdot\left(-4\right)=5\\ \Delta'>0\\ \Rightarrow x_1=\dfrac{-b'+\sqrt{\Delta'}}{a}=1+\sqrt{5}\\ x_2=\dfrac{-b'-\sqrt{\Delta'}}{a}=1-\sqrt{5}\)
Chương I - Căn bậc hai. Căn bậc ba
Đúng 1
Bình luận (0)
Các câu hỏi tương tự
Cho a,b ,c là các số thực thỏa mãn (a-b)(a-c)=1 b khác c. Chứng minh
\(\frac{1}{\left(a-b\right)^2}+\frac{1}{\left(b-c\right)^2}+\frac{1}{\left(c-a\right)^2}\ge4\)
\(\sqrt{4x^2-4x+1}=x-1\)
Tìm ĐK
Câu 1: Rút gọn biểu thức:
a) \(\sqrt{19+\sqrt{136}}-\sqrt{19-\sqrt{136}}\)
b) \(\sqrt{27}+\sqrt{-64}+2\sqrt{125}\)
Câu 2: Tìm x biết:
\(\sqrt{4x+20}-2\sqrt{x+5}+\sqrt{9x+45}=6\)
Rút gọn
\(A=\frac{\sqrt{x}}{\sqrt{x}-2}+\frac{\sqrt{x}-1}{\sqrt{x}+2}+\frac{\sqrt{x}-10}{x-4}\) (x\(\ge\)0, x \(\ne\) 4)
\(B=\left(13-4\sqrt{3}\right)\left(7+4\sqrt{3}\right)-8\sqrt{20+2\sqrt{43+24\sqrt{3}}}\)
Tìm giá trị nhỏ nhất của biểu thức P=\(\frac{1}{a}+\frac{1}{b}\)Cho a+b nhỏ hơn bằng \(2\sqrt{2}\)
Dạ mọi người giup em bài này với ạ. Dạ em cảm ơn ạ
So sánh
\(\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{2004}}\) và 86
1) Cho x,y,z -1 thỏa mãn:
x^3+y^3+z^3≥ x^2+y^2+z^2
CMR: x^5+y^5+z^5≥ x^2+y^2+z^2
2. Cho a,b,c ϵ {0;1;2} và a+b+c3
CMR: a^2+b^2+c^2 ≤ 5
3. Cho a_1,a_2,..,a_9inleft[-1;1right] sao cho a^3_1+a^3_2+...+a^3_90
CMR: a^3_1+a^3_2+...+a^3_9le3
4. Cho abge1. CMR: frac{1}{a^2+1}+frac{1}{b^2+1}gefrac{2}{1+ab}
5. Cho a,b,c 0. CMR:
frac{a^2+b^2}{a+b}+frac{b^2+c^2}{b+c}+frac{c^2+a^2}{c+a}le3cdotfrac{a^2+b^2+c^2}{a+b+c}
Đọc tiếp
1) Cho x,y,z > -1 thỏa mãn:
\(x^3+y^3+z^3\)≥ \(x^2+y^2+z^2\)
CMR: \(x^5+y^5+z^5\)≥ \(x^2+y^2+z^2\)
2. Cho a,b,c ϵ {0;1;2} và a+b+c=3
CMR: \(a^2+b^2+c^2\) ≤ 5
3. Cho \(a_1,a_2,..,a_9\in\left[-1;1\right]\) sao cho \(a^3_1+a^3_2+...+a^3_9=0\)
CMR: \(a^3_1+a^3_2+...+a^3_9\le3\)
4. Cho \(ab\ge1\). CMR: \(\frac{1}{a^2+1}+\frac{1}{b^2+1}\ge\frac{2}{1+ab}\)
5. Cho a,b,c >0. CMR:
\(\frac{a^2+b^2}{a+b}+\frac{b^2+c^2}{b+c}+\frac{c^2+a^2}{c+a}\le3\cdot\frac{a^2+b^2+c^2}{a+b+c}\)
Tính \(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\)
Tìm giá trị nhỏ nhất của biểu thức
a) x -\(\sqrt{x}\) + 1
b) 4x\(^2\) + 4x + 4
c) 2x - 2\(\sqrt{x}\) + 3
d) x\(^2\) - x\(\sqrt{3}\) + 1
mng giúp em với ạ T_T