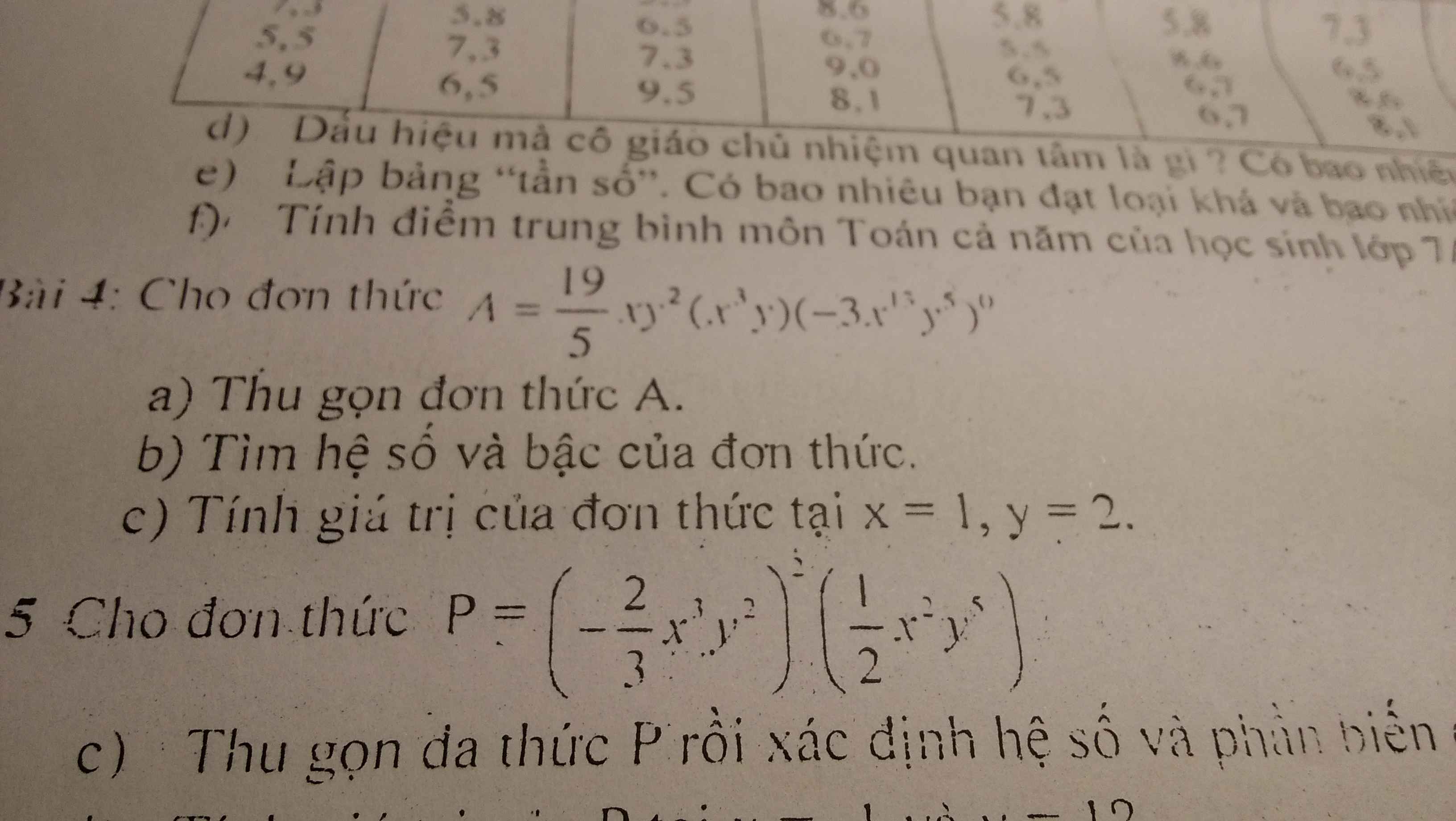a: Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=3^2+4^2=25\)
=>\(BC=\sqrt{25}=5\left(cm\right)\)
b: Xét ΔABD và ΔAID có
AB=AI
\(\widehat{BAD}=\widehat{IAD}\)(AD là phân giác của góc BAC)
AD chung
Do đó: ΔABD=ΔAID
=>DB=DI
c: Ta có: ΔABD=ΔAID
=>\(\widehat{ABD}=\widehat{AID}\)
Ta có: \(\widehat{ABD}+\widehat{DBK}=180^0\)(hai góc kề bù)
\(\widehat{AID}+\widehat{CID}=180^0\)(hai góc kề bù)
mà \(\widehat{ABD}=\widehat{AID}\)
nên \(\widehat{CID}=\widehat{KBD}\)
Xét ΔDBK và ΔDIC có
\(\widehat{DBK}=\widehat{DIC}\)
DB=DI
\(\widehat{BDK}=\widehat{IDC}\)(hai góc đối đỉnh)
Do đó ΔDBK=ΔDIC
=>BK=IC
Ta có: AB+BK=AK
AI+IC=AC
mà AB=AI và BK=IC
nên AK=AC
=>ΔAKC cân tại A
Xét ΔAKC cân tại A có \(\widehat{KAC}=90^0\)
nên ΔAKC vuông cân tại A