\(\dfrac{x-1}{3x^2-4x+1}>\dfrac{2}{6x-5}.\left(x\ne\dfrac{5}{6};1;\dfrac{1}{3}\right).\)
\(\Leftrightarrow\dfrac{x-1}{\left(x-1\right)\left(x-\dfrac{1}{3}\right)}-\dfrac{2}{6x-5}>0.\\ \Leftrightarrow\dfrac{1}{x-\dfrac{1}{3}}-\dfrac{2}{6x-5}>0.\)
\(\Leftrightarrow\dfrac{6x-5-2x+\dfrac{2}{3}}{\left(x-\dfrac{1}{3}\right)\left(6x-5\right)}>0.\\ \Leftrightarrow\dfrac{4x-\dfrac{13}{3}}{\left(x-\dfrac{1}{3}\right)\left(6x-5\right)}>0.\)
Đặt \(f\left(x\right)=\dfrac{4x-\dfrac{13}{3}}{\left(x-\dfrac{1}{3}\right)\left(6x-5\right)}.\)
Ta có:
\(4x-\dfrac{13}{3}=0.\Leftrightarrow x=\dfrac{13}{12}.\\ x-\dfrac{1}{3}=0.\Leftrightarrow x=\dfrac{1}{3}.\\ 6x-5=0.\Leftrightarrow x=\dfrac{5}{6}.\)
Bảng xét dấu:
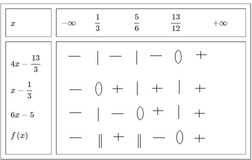
\(\Rightarrow\) \(f\left(x\right)>0\Rightarrow x\in\left(\dfrac{1}{3};\dfrac{5}{6}\right)\cup[\dfrac{13}{12};+\infty).\)















