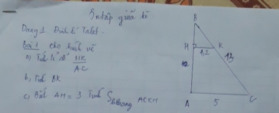
a) \(\dfrac{HK}{AC}=\dfrac{1,2}{5}=\dfrac{6}{25}.\)
b) Xét \(\Delta ABC:\)
\(BC^2=13^2=169.\\ AB^2+AC^2=12^2+5^2=169.\\ \Rightarrow BC^2=AB^2+AC^2.\)
\(\Rightarrow\Delta ABC\) vuông tại A.
\(\Rightarrow\widehat{BAC}=90^o.\)
Ta có: \(HK\perp AB\left(gt\right).\\ AC\perp AB\left(\widehat{BAC}=90^o\right).\)
\(\Rightarrow HK//AC.\)
Xét \(\Delta ABC\) vuông tại A:
\(HK//AC\left(cmt\right).\\ \Rightarrow\dfrac{BK}{BC}=\dfrac{HK}{AC}\left(Talet\right).\)
\(\Rightarrow\dfrac{BK}{13}=\dfrac{6}{25}.\\ \Rightarrow BK=3,12.\)
c) Ta có: \(S_{ACHK}=\dfrac{\left(HK+AC\right).AH}{2}=\dfrac{\left(1,2+5\right).3}{2}=9,3.\)
a, Ta có \(\dfrac{HK}{AC}=\dfrac{1,2}{5}=\dfrac{6}{25}\)
b, Theo hệ quả Ta lét ta có
\(\dfrac{BK}{13+BK}=\dfrac{6}{25}\Rightarrow25BK=78+6BK\Leftrightarrow19BK=78\Leftrightarrow BK=\dfrac{78}{19}\)
c, \(S_{AHKC}=\dfrac{HK+AC}{2}.3=\dfrac{93}{10}\)(đvdt)