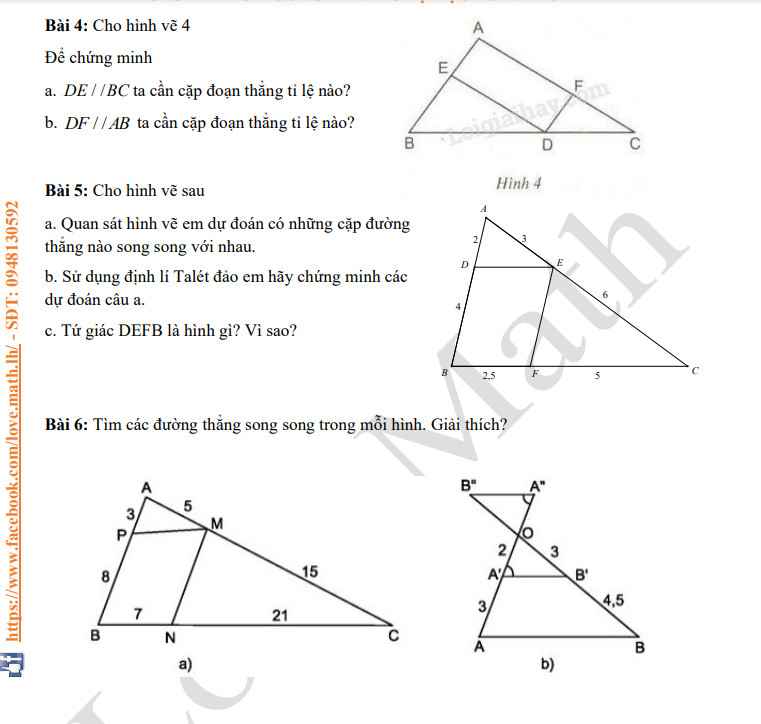
\(4.\\ a)DE//AC.\Leftrightarrow\dfrac{BE}{BA}=\dfrac{BD}{BC}\left(Talet\right).\\ b)DF//AB.\Leftrightarrow\dfrac{CF}{CA}=\dfrac{CD}{CB}\left(Talet\right).\)
\(5.\)
\(a)\) Xét \(\Delta ACB:\)
\(\dfrac{AM}{MC}=\dfrac{5}{15}=\dfrac{1}{3}.\\ \dfrac{BN}{NC}=\dfrac{7}{21}=\dfrac{1}{3}.\\ \Rightarrow\dfrac{AM}{MC}=\dfrac{BN}{NC}.\)
\(\Rightarrow MN//AB\left(Talet\right).\)
\(b)\) Xét \(\Delta OAB:\)
\(\dfrac{OA'}{A'A}=\dfrac{2}{3}.\\ \dfrac{OB'}{B'B}=\dfrac{3}{4,5}=\dfrac{2}{3}.\\ \Rightarrow\dfrac{OA'}{A'A}=\dfrac{OB'}{B'B}.\)
\(\Rightarrow A'B'//AB\left(Talet\right).\) (1)
Ta có: \(\widehat{B''A''O}=\widehat{OA'B'}\) (Theo hình vẽ).
\(\Rightarrow B''A''//A'B'.\) (2)
Từ (1) và (2) \(\Rightarrow AB//A'B'//A''B''.\)