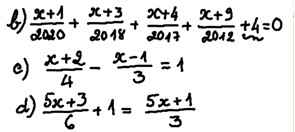\(b,\Rightarrow\left(\dfrac{x+1}{2020}+1\right)+\left(\dfrac{x+3}{2018}+1\right)+\left(\dfrac{x+4}{2017}+1\right)+\left(\dfrac{x+9}{2012}+1\right)=0\\ \Rightarrow\dfrac{x+2021}{2020}+\dfrac{x+2021}{2018}+\dfrac{x+2021}{2017}+\dfrac{x+2021}{2012}=0\\ \Rightarrow\left(x+2021\right)\left(\dfrac{1}{2020}+\dfrac{1}{2018}+\dfrac{1}{2017}+\dfrac{1}{2012}\right)=0\\ \Rightarrow x+2021=0\\ \Rightarrow x=-2021\)
\(c,\Rightarrow\dfrac{x+2}{4}-\left(\dfrac{x-1}{3}+1\right)=0\\ \Rightarrow\dfrac{x+2}{4}-\dfrac{x+2}{3}=0\\ \Rightarrow\left(x+2\right)\left(\dfrac{1}{4}-\dfrac{1}{3}\right)=0\\ \Rightarrow x+2=0\\ \Rightarrow x=-2\\ d,\Rightarrow\dfrac{5x+9}{6}=\dfrac{5x+1}{3}\\ \Rightarrow3\left(5x+9\right)=6\left(5x+1\right)\\ \Rightarrow15x+27=30x+6\\ \Rightarrow15x=21\\ \Rightarrow x=\dfrac{7}{5}\)