Bài 4: Góc tạo bởi tiếp tuyến và dây cung
Các câu hỏi tương tự
Giả sử A và B là hai điểm phân biệt trên đường tròn (O).Các tiếp tuyến của đường tròn (O) tại A và B cách nhau tại M. Từ A kẻ đường thẳng song song với MB, cắt (O) tại C .MC cắt đường tròn (O) tại E. Các tia AE và MB cắt nhau tại K. Chứng minh rằng:
1) MK2 = AK . EK
2) MK = KB
Từ một điểm M cố định ở bên ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó.
a) Chứng minh rằng ta luôn có MT^2MA.MB và tích này không phụ thuộc vị trí của cát tuyến MAB
b) Ở hình 2, khi cho MT 20 cm, MB 50 cm, tính bán kính đường tròn ?
Đọc tiếp
Từ một điểm M cố định ở bên ngoài đường tròn (O) ta kẻ một tiếp tuyến MT và một cát tuyến MAB của đường tròn đó.
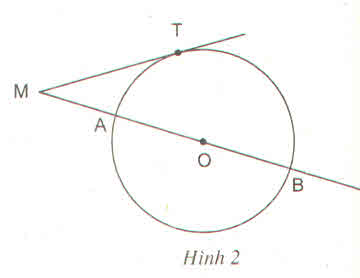
a) Chứng minh rằng ta luôn có \(MT^2=MA.MB\) và tích này không phụ thuộc vị trí của cát tuyến MAB
b) Ở hình 2, khi cho MT = 20 cm, MB = 50 cm, tính bán kính đường tròn ?
Hai đường tròn (O) và (O) cắt nhau tại A và B. Qua A vẽ cát tuyến CAD với hai đường tròn left(Cinleft(Oright),Dinleft(Oright)right)
a) Chứng minh rằng khi cát tuyến quay xung quanh điểm A thì widehat{CBD} có số đo không đổi
b) Từ C và D vẽ hai tiếp tuyến với đường tròn. Chứng minh rằng hai tiếp tuyến này hợp với nhau một góc có số đo không đổi khi cát tuyến CAD quay xung quanh điểm A
Đọc tiếp
Hai đường tròn (O) và (O') cắt nhau tại A và B. Qua A vẽ cát tuyến CAD với hai đường tròn \(\left(C\in\left(O\right),D\in\left(O'\right)\right)\)
a) Chứng minh rằng khi cát tuyến quay xung quanh điểm A thì \(\widehat{CBD}\) có số đo không đổi
b) Từ C và D vẽ hai tiếp tuyến với đường tròn. Chứng minh rằng hai tiếp tuyến này hợp với nhau một góc có số đo không đổi khi cát tuyến CAD quay xung quanh điểm A
Cho BC là dây cung cố định của đường tròn (O) cố định.Gọi I là điểm chính giữa của cung lớn BC.Vẽ đường tròn tâm I bán kính IB=IC.Điểm A di động trên cung lớn BC của (O).Tia BA cắt (I) tại D
1. Chứng minh AC=AD
2.Tìm vị trí điểm A trên BC để chu vi tam giác ABC lớn nhất
Cho nửa đường tròn (O) đường kính AB. Trên tia đối của tia AB lấy một điểm M. Vẽ tiếp tuyến MC với nửa đường tròn. Gọi H là hình chiếu của C trên AB
Giúp mik giải câu c phần định lí bài góc tạo bởi tia tiếp tuyến và dây cung
Giúp mik đi mai mik ktra 15p òi.😟
Xem chi tiết
cho đường tròn tâm O hai đường kính AB, CD vuông góc với nhau. tiếp tuyến tại M trên cung nhỏ AC cắt DC tại K. C/m MKD=2MDA
Cho đường thẳng (d) không cắt đường tròn (O), vẽ đường kính CD vuông góc với đường thẳng d tại I. Kẻ tiếp tuyến IA với đường tròn (O). Đường thẳng CA cắt đường thẳng d tại B. Chứng minh IA = IB.
cho nửa đường tròn tâm o đường kính AB=2R. Trên nữa mặt phẳng chứa đường tròn dựng tia tiếp tuyến Ax, từ điểm M trên tia Ax kẻ tiếp tuyến thứ 2 là MC với nữa đường tròn, đường thẳng BC cắt Ax tại D. a.Chứng minh M là trung điểm của AD. b.Giả sử góc BAC=30°, chứng minh MO=2AC.
c.Tính diện tích tam giác ABD theo R
Xem chi tiết
bài 1:Cho tam giác ABC vuông tại B có BA=18 cm, BC=24cm. tính chu vi của đường tròn ngoại tiếp tam giác ABC
bài 2: cho hình thang vuông ABCD vuông tại A và D. gọi O là trung điểm của AD và BOC=90 độ. Gọi E là giao điểm của BO và CD. chứng minh rằng
a) tam giác BCE cân tại C
b) BC là tiếp tuyến của đường tròn đường kính AD











