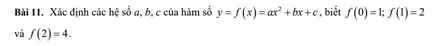\(f\left(0\right)=1\Leftrightarrow c=1\left(1\right)\\ f\left(1\right)=2\Leftrightarrow a+b+c=2\left(2\right)\\ f\left(2\right)=4\Leftrightarrow4a+2b+c=4\left(3\right)\\ \left(1\right)\left(2\right)\left(3\right)\Leftrightarrow\left\{{}\begin{matrix}c=1\\a+b+1=2\\4a+2b+1=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a+b=1\\4a+2b=3\\c=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=\dfrac{1}{2}\\c=1\end{matrix}\right.\)
Vậy \(y=f\left(x\right)=\dfrac{1}{2}x^2+\dfrac{1}{2}x+1\)
\(\left\{{}\begin{matrix}f\left(0\right)=c=1\\f\left(1\right)=a+b+c=2\\f\left(2\right)=4a+2b+c=4\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}a+b=1\\4a+2b=3\end{matrix}\right.\)\(\Rightarrow a=b=\dfrac{1}{2}\)
Vậy (a;b;c)=\(\left(\dfrac{1}{2};\dfrac{1}{2};1\right)\)