\(1,\Rightarrow x^2+4x+4-x^2=3\Rightarrow4x=-1\Rightarrow x=-\dfrac{1}{4}\\ 2,\Rightarrow4x^2+x-4x^2+4x-1=0\Rightarrow5x=1\Rightarrow x=\dfrac{1}{5}\\ 3,\Rightarrow x^2-3x-x^2+2x-1=0\Rightarrow x=-1\\ 4,\Rightarrow4x^2-2x+\dfrac{1}{4}-2x^2+x+3=0\\ \Rightarrow2x^2-x+\dfrac{13}{4}=0\\ \Rightarrow2\left(x^2-\dfrac{1}{2}x+\dfrac{1}{16}\right)+\dfrac{51}{16}=0\\ \Rightarrow2\left(x-\dfrac{1}{4}\right)^2+\dfrac{51}{16}=0\left(vô.lí\right)\\ \Rightarrow x\in\varnothing\)
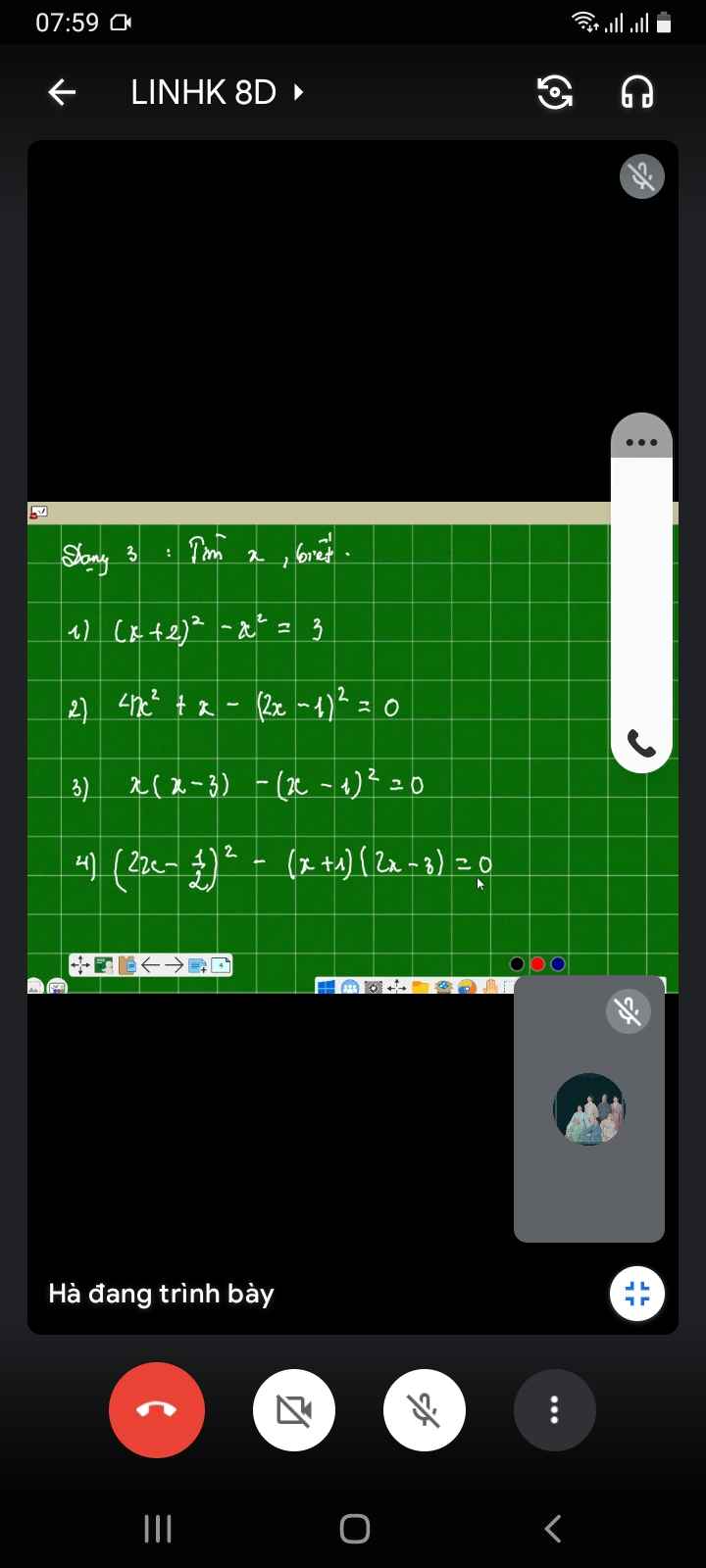
1) \(\Leftrightarrow x^2+4x+4-x^2=3\)
\(\Leftrightarrow4x=-1\Leftrightarrow x=-\dfrac{1}{4}\)
2) \(\Leftrightarrow4x^2+x-4x^2+4x-1=0\)
\(\Leftrightarrow5x=1\Leftrightarrow x=\dfrac{1}{5}\)
3) \(\Leftrightarrow x^2-3x-x^2+2x-1=0\)
\(\Leftrightarrow x=-1\)
4) \(\Leftrightarrow4x^2-2x+\dfrac{1}{4}-2x^2+x+3=0\)
\(\Leftrightarrow2x^2-x+\dfrac{13}{4}=0\)
\(\Leftrightarrow2\left(x^2-\dfrac{1}{2}x+\dfrac{1}{16}\right)+\dfrac{25}{8}=0\)
\(\Leftrightarrow2\left(x-\dfrac{1}{4}\right)^2+\dfrac{25}{8}=0\)( vô lý do \(2\left(x-\dfrac{1}{4}\right)^2+\dfrac{25}{8}\ge\dfrac{25}{8}>0\))
Vậy \(S=\varnothing\)