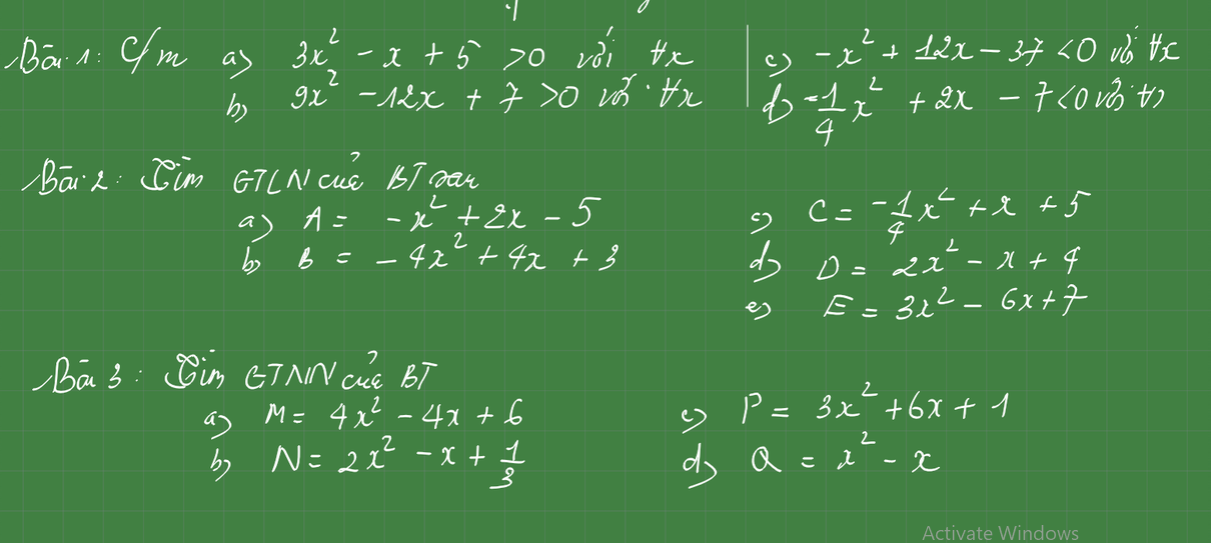\(1,\\ a,3x^2-x+5=3\left(x^2-\dfrac{1}{3}x+\dfrac{1}{36}+\dfrac{59}{36}\right)\\ =3\left(x+\dfrac{1}{6}\right)^2+\dfrac{59}{12}\ge\dfrac{59}{12}>0\\ b,9x^2-12x+7=\left(3x-2\right)^2+3\ge3>0\\ c,-x^2+12x-37=-\left(x-6\right)^2-1\le-1< 0\\ d,-\dfrac{1}{4}x^2+2x-7=-\left(\dfrac{1}{4}x^2+2x+4\right)-3\\ =-\left(\dfrac{1}{2}x+2\right)^2-3\le-3< 0\)
\(2,\\ a,A=-x^2+2x-5=-\left(x-1\right)^2-4\le-4\)
Dấu \("="\Leftrightarrow x=1\)
\(b,B=-4x^2+4x+3=-\left(2x-1\right)^2+4\le4\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{2}\)
\(c,C=-\dfrac{1}{4}x^2+x+5=-\left(\dfrac{1}{4}x+x+1\right)+6=-\left(\dfrac{1}{2}x+1\right)^2+6\le6\)
Dấu \("="\Leftrightarrow\dfrac{1}{2}x=-1\Leftrightarrow x=-2\)
\(d,D=2x^2-x+4=2\left(x^2-\dfrac{1}{2}x+\dfrac{1}{16}+\dfrac{31}{16}\right)=2\left(x-\dfrac{1}{4}\right)^2+\dfrac{31}{8}\ge\dfrac{31}{8}\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{4}\)
\(e,E=3x^2-6x+7=3\left(x-1\right)^2+4\ge4\)
Dấu \("="\Leftrightarrow x=1\)
\(3,\\ a,M=4x^2-4x+6=\left(2x-1\right)^2+5\ge5\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{2}\)
\(b,N=2x^2-x+\dfrac{1}{3}=2\left(x^2-\dfrac{1}{2}x+\dfrac{1}{16}+\dfrac{5}{48}\right)=2\left(x-\dfrac{1}{4}\right)^2+\dfrac{5}{24}\ge\dfrac{5}{24}\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{4}\)
\(c,P=3x^2+6x+1=3\left(x+1\right)^2-2\ge-2\)
Dấu \("="\Leftrightarrow x=-1\)
\(d,Q=x^2-x=\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{2}\)