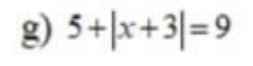\(5+\left|x+3\right|=9\)
\(\Leftrightarrow\left|x+3\right|=4\)
\(\Leftrightarrow x+3=\pm4\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-7\end{matrix}\right.\)
5 + Ix + 3I = 9
Ix + 3 I = 9 -5
Ix + 3 I = 4
=> x + 3 = -+4
x = 4 - 3
x = 1
x + 3 = -4
x = -4 -3
x= -7
Vậy x={ .....}
\(5+|x+3|=9\\ \Leftrightarrow|x+3|=4\\ \Leftrightarrow\left[{}\begin{matrix}x+3=4\\x+3=-4\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-7\end{matrix}\right.\)
\(\left[{}\begin{matrix}\\\end{matrix}\right.\)là hoặc nha bn
tik mik nha
Ta có 2 TH:
Nếu x \(\ge\) -3 thì \(|x+3|=x+3\)
Nếu x < -3 thì \(|x+3|=-\left(x+3\right)\)
TH1:
Nếu x \(\ge\) -3:
5 + x + 3 = 9
<=> x = 9 - 5 - 3
<=> x = 1 (thỏa mãn)
Vậy x = 1
TH2: Nếu x < -3:
5 + \(\left[-\left(x+3\right)\right]=9\)
<=> 5 + (x - 3) = 9
<=> 5 + x - 3 = 9
<=> x = 9 - 5 + 3
<=> x = 7 (loại)
Vậy PT có nghiệm duy nhất S = \(\left\{1\right\}\)
g: Ta có: \(5+\left|x+3\right|=9\)
\(\Leftrightarrow\left|x+3\right|=4\)
\(\Leftrightarrow\left[{}\begin{matrix}x+3=4\\x+3=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-7\end{matrix}\right.\)