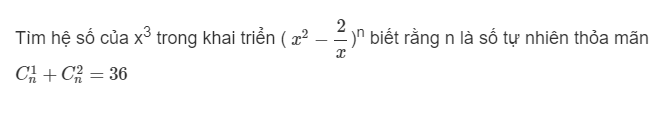\(C^1_n+C^2_n=36\)
\(\Leftrightarrow\dfrac{n!}{\left(n-1\right)!}+\dfrac{n!}{2.\left(n-2\right)!}=36\)
\(\Leftrightarrow n+\dfrac{\left(n-1\right)n}{2}=36\)
\(\Leftrightarrow n^2+n-72=0\)
\(\Leftrightarrow\left[{}\begin{matrix}n=8\\n=-9\left(l\right)\end{matrix}\right.\)
Khi đó:
\(\left(x^2-\dfrac{2}{x}\right)^8=\sum\limits^8_{k=0}C_8^k.\left(x^2\right)^{8-k}.\left(-\dfrac{2}{x}\right)^k\)
\(=\sum\limits^8_{k=0}\left(-2\right)^k.C_8^k.x^{16-2k}.\dfrac{1}{x^k}\)
\(=\sum\limits^8_{k=0}\left(-2\right)^k.C_8^k.x^{16-3k}\)
Số hạng \(x^3\) tương ứng với k: \(16-3k=3\Leftrightarrow k=\dfrac{13}{3}\)
Đề có sai không vậy?