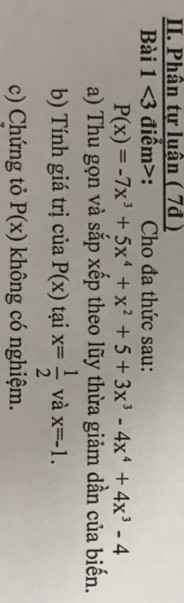a) \(P\left(x\right)=-7x^3+5x^4+x^2+5+3x^3-4x^4+4x^3-4\)
\(\Rightarrow P\left(x\right)=\left(-7x^3+3x^3+4x^3\right)+\left(5x^4-4x^4\right)+x^2+\left(5-4\right)\)
\(\Rightarrow P\left(x\right)=x^4+x^2+1\)
b) Xét \(x=\dfrac{1}{2}\) \(\Rightarrow P\left(\dfrac{1}{2}\right)=\left(\dfrac{1}{2}\right)^4+\left(\dfrac{1}{2}\right)^2+1\) \(\Rightarrow P\left(\dfrac{1}{2}\right)=\dfrac{1}{16}+\dfrac{1}{4}+1=\dfrac{21}{16}\)
Xét \(x=-1\) \(\Rightarrow P\left(-1\right)=\left(-1\right)^4+\left(-1\right)^2+1\) \(\Rightarrow P\left(-1\right)=1+1+1=3\)
c) Ta có P(x) = x4 + x2 + 1
Vì \(x^4\ge0;x^2\ge0\) với \(\forall x\in R\) \(\Rightarrow x^4+x^2\ge0\) với \(\forall x\in R\)
\(\Rightarrow x^4+x^2+1\ge1\) với \(\forall x\in R\) \(\Rightarrow x^4+x^2+1>0\) với \(\forall x\in R\)
\(\Rightarrow P\left(x\right)>0\) \(\Rightarrow\) Đa thức P(x) không có nghiệm