Học tại trường
Chưa có thông tin
Đến từ
Thành phố Hồ Chí Minh , Chưa có thông tin
Số lượng câu hỏi
125
Số lượng câu trả lời
16150
Điểm GP
2611
Điểm SP
23866
Người theo dõi (633)
Đang theo dõi (4)

Câu trả lời:
\(PTK_{BaCl_2}=137+35,5\cdot2=208\)


Câu trả lời:
D
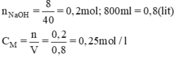


Câu trả lời:
When did he go to Ha Noi?