Tham khảo: 

Trong cuộc sống của chúng ta không thể nào thiếu được lòng tốt, tình yêu thương bởi nó là thứ tình cảm gắn kết con người gần nhau hơn. Và một trong những câu chuyện đã truyền cảm hứng về tình người cho em đó là câu chuyện “Tờ báo tường của tôi” của tác giả Nguyễn Luân. Câu chuyện đã cho chúng ta một bài học tình người vô cùng quý giá.

Ngay từ lần đầu tiên đọc câu chuyện, em đã rất ấn tượng. Bởi câu chuyện đã đề cập bài học sâu sắc về tình người, giúp đỡ người khác lúc khó khăn. Không chỉ vậy, câu chuyện còn có một chi tiết cảm động đối với em. Đó là chi tiết mặc dù trời nhá nhem tối, khu rừng âm u nhưng cậu bé vẫn vượt qua nỗi sợ hãi để băng qua rừng thật nhanh vì người bị nạn. “Trời bắt đầu nhá nhem tối. Khu rừng âm u. Tiếng mấy con chim kêu “túc... túc...” không ngớt. Tôi chạy nhanh hơn. Gió thổi vù vù bên tai, bàn chân đau nhói vì giẫm lên đá răng mèo. “Phải cố lên! Người bị nạn nguy mất...”.” Chính nhờ sự dũng cảm, gan dạ và lòng tốt của cậu bé mà người bị nạn đã nhanh chóng được các chú bộ đội biên phòng cứu giúp.

Câu chuyện “Tờ báo tường của tôi” đã truyền không chỉ cho em mà cho tất cả mọi người bài học về lòng tốt. Em hứa sẽ giống như cậu bé trong câu chuyện, sẵn sàng giúp đỡ người khác lúc khó khăn..

Văn bản trên giới thiệu trò chơi gì và của dân tộc nào?

A. Đánh khăng của người Kinh

B. Đánh trỏng của người Khmer

C. Đánh kol của người Khmer

D. Đánh kol của người Chăm

Theo văn bản, phần lớn người Khmer cư trú và sinh sống ở đâu?

A. Nam Trung Bộ

B. Đồng bằng sông Cửu Long

C. Kon Tum

D. Đông Nam B

a) Sự khác biệt giữa hai đại lượng đã cho là:

- Bác Ba có số tiền là 20 triệu đồng, đại lượng này là một đại lượng vô hướng vì nó chỉ số tiền nên nó chỉ có độ lớn.

- Một cơn bão di chuyển với vận tốc 20 km/h theo hướng đông bắc, đại lượng này là một đại lượng có hướng vì nó có đề cập đến độ lớn và hướng.

b) Trong các đại lượng đã cho, các đại lượng lực, độ dịch chuyển, vận tốc là các đại lượng có hướng, chúng bao gồm cả độ lớn và hướng nên các đại lượng đó cần được biểu diễn bởi vectơ.

Giúp với

a) Số máy tính loại A cửa hàng cần nhập trong một tháng là x (máy), số máy tính loại B cửa hàng cần nhập trong một tháng là y (máy) .

Do tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy: x + y ≤ 250

Tổng số vốn cửa hàng cần nhập hai loại A và B: 10x + 20y (triệu đồng)

Vì mỗi chiếc máy tính loại A có giá 10 triệu và mỗi máy tính loại B có giá 20 triệu nên tổng số vốn cửa hàng cần nhập hai loại A và B: 10x + 20y (triệu đồng)

Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên ta có: 10x + 20y ≤ 4 000 hay x + 2y ≤ 400.

Ta có hệ bất phương trình: \(\left\{{}\begin{matrix}x\ge0\\y\ge0\\x+y\le250\\x+2y\le400\end{matrix}\right.\)

Ta xác định miền nghiệm của hệ bất phương trình trên:

+) Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1;0).

+) Miền nghiệm D2 của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0;1).

+) Xác định miền nghiệm D3 của bất phương trình x + y ≤ 250.

- Vẽ đường thẳng d: x + y = 250.

- Vì 0 + 0 = 0 < 250 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + y ≤ 250

Do đó miền nghiệm D3 của bất phương trình x + y ≤ 250 là nửa mặt phẳng bờ d chứa gốc tọa độ.

+) Xác định miền nghiệm D4 của bất phương trình x + 2y ≤ 400.

- Vẽ đường thẳng d’: x + 2y  = 400.

- Vì 0 + 2.0 = 0 < 400 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + 2y < 400

Do đó miền nghiệm D4 của bất phương trình x + 2y < 400 là nửa mặt phẳng bờ d’ chứa gốc tọa độ.

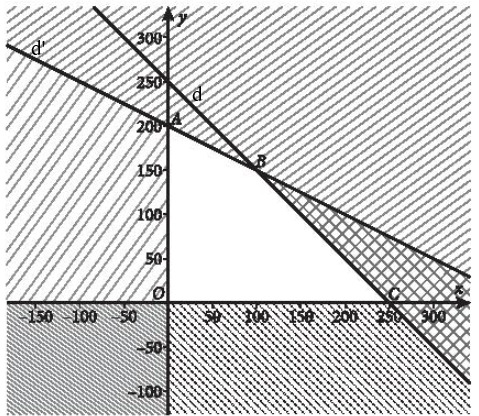
Miền nghiệm của hệ bất phương trình trên là tứ giác OABC với O(0;0), A(0; 200), C(100;150), B(250;0)

b) Lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B là: F(x;y) = 2,5x + 4y (triệu đồng).

Vậy F(x;y) = 2,5x + 4y.

c) Bài toán chuyển về tìm giá trị lớn nhất của F(x;y) với (x;y) thuộc miền nghiệm của hệ bất phương trình \(\left\{{}\begin{matrix}x\ge0\\y\ge0\\x+y\le250\\x+2y\le400\end{matrix}\right.\)

Người ta đã chứng minh được, giá trị F(x; y) lớn nhất tại (x; y) là tọa độ của một trong bốn đỉnh O; A; B; C.

Tại O(0; 0), ta có: F(0; 0) = 2,5 . 0 + 4 . 0 = 0;

Tại A(0; 200), ta có: F(0; 200) = 2,5 . 0 + 4 . 200 = 800;

Tại B(100; 150), ta có: F(100; 150) = 2,5 . 100 + 4 . 150 = 850;

Tại B(250; 0), ta có: F(250; 0) = 2,5 . 250 + 4 . 0 = 625.

Do đó F(x;y) lớn nhất bằng 850 tại x = 100 và y = 150.

Vậy cửa hàng cần nhập 100 máy loại A, 150 máy loại B để cửa hàng thu được lợi nhuận lớn nhất là 850 triệu đồng.