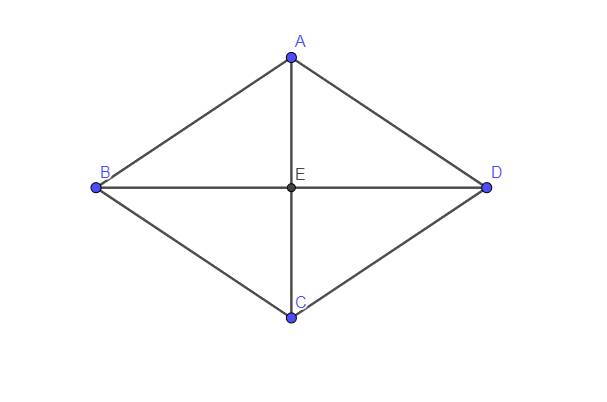
Câu trả lời:
\(AE=\dfrac{AC}{2}=\dfrac{4}{2}=2\left(cm\right)\)
\(BE=\dfrac{BD}{2}=\dfrac{6}{2}=3\left(cm\right)\)
Áp dụng định lí Py - ta - go vào \(\Delta ABE\) vuộng tại \(E\)
\(BE^2+AE^2=AB^2\)
\(\rightarrow AB=\sqrt{BE^2+AE^2}=\sqrt{3^2+2^2}=\sqrt{13}\left(cm\right)\)
\(\rightarrow P_{ABCD}=AB.4=\sqrt{13}.4=4\sqrt{13}\left(cm\right)\)
Vậy chu vi hình thoi là \(4\sqrt{13}\left(cm\right)\)