Học tại trường
Chưa có thông tin
Đến từ
Thanh Hóa , Chưa có thông tin
Số lượng câu hỏi
18
Số lượng câu trả lời
1194
Điểm GP
110
Điểm SP
526
Người theo dõi (15)
Đang theo dõi (24)

Câu trả lời:
𝕙𝕒𝕖𝕟𝕘𝟚𝟘𝟙𝟘


Câu trả lời:
Bạn cung cấp thêm thông tin để người ta trả lời ạ.

Câu trả lời:
`C`

Câu trả lời:
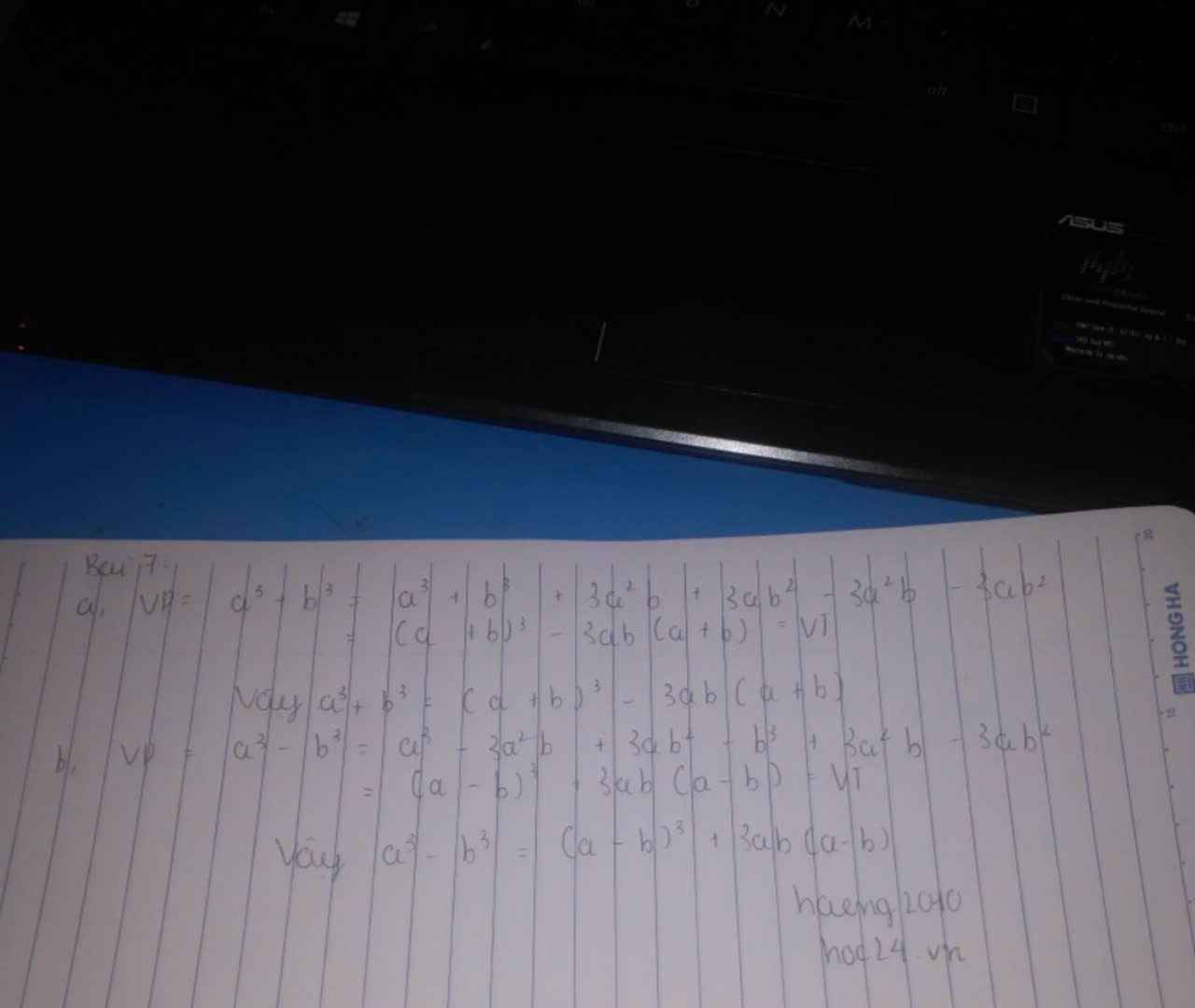
𝕙𝕒𝕖𝕟𝕘𝟚𝟘𝟙𝟘













