Cho hàm số f(x) = 2x + ex. Nguyên hàm F(x) của hàm số f(x) trên ℝ sao cho F(0) = 2 023 là:
A. x2 + ex + 2 023. B. x2 + ex + C.
C. x2 + ex + 2 022. D. x2 + ex.
Cho hàm số f(x) = 2x + ex. Nguyên hàm F(x) của hàm số f(x) trên ℝ sao cho F(0) = 2 023 là:
A. x2 + ex + 2 023. B. x2 + ex + C.
C. x2 + ex + 2 022. D. x2 + ex.
Giả sử A, B lần lượt là diện tích các hình được tô màu ở Hình 37.
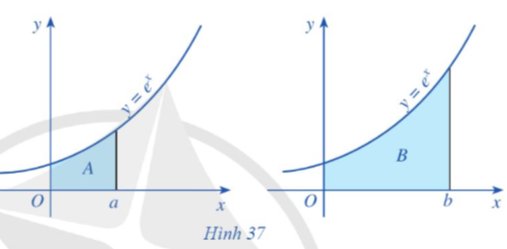
a) Tính các diện tích A, B.
b) Biết B = 3A. Biểu diễn b theo a.
Thảo luận (1)Hướng dẫn giảia) \(A = \int\limits_0^a {{e^x}} dx\)
\(B = \int\limits_0^b {{e^x}} dx\)
b) \(B = 3A \Leftrightarrow \int\limits_0^b {{e^x}} dx = 3\int\limits_0^a {{e^x}} dx \Leftrightarrow \left. {{e^x}} \right|_0^b = 3\left. {{e^x}} \right|_0^a \Leftrightarrow {e^b} - 1 = 3{e^a} - 3 \Leftrightarrow b = \ln (3{e^a} - 2)\)
(Trả lời bởi Nguyễn Quốc Đạt)
Hình 38 minh họa mặt cắt đứng của một bức tường cũ có dạng hình chữ nhật với một cổng ra vào có dạng hình parabol với các kích thước được cho như trong hình đó. Người ta dự định sơn lại mặt ngoài của bức tường đó. Chi phí để sơn bức tường là 15 000 đồng/1 m2. Tổng chi phí để sơn lại toàn bộ mặt ngoài của bức tường đó sẽ là bao nhiêu?
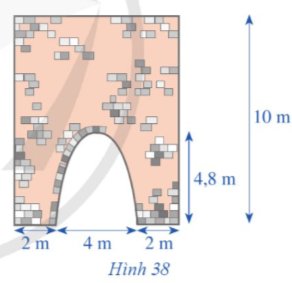
Thảo luận (1)Hướng dẫn giảiChọn hệ tọa độ Oxy có gốc tọa độ O(0;0) tại chân bên trái của bức tường
Cổng được biểu diễn trên hệ tọa độ bằng hàm số: \(y = a{x^2} + b\)
Đồ thị hàm số này đi qua điểm (2;0) và có đỉnh là (4;4,8), ta có: \(\left\{ \begin{array}{l}4a + b = 0\\16a + b = 4,8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0,4\\b = - 1,6\end{array} \right.\)
Vậy \(y = 0,4{x^2} - 1,6\)
Diện tích cánh cổng là: \(\int\limits_2^6 {\left( {0,4{x^2} - 1,6} \right)dx} = \left. {\left( {\frac{2}{{15}}{x^3} - 1,6x} \right)} \right|_2^6 = \frac{{64}}{3}{m^2}\)
Diện tích bức tường là: 10.8 = 80\({m^2}\)
Diện tích cần sơn là: \(80 - \frac{{64}}{3} = \frac{{176}}{3}{m^2}\)
Tổng chi phí để sơn lại toàn bộ mặt ngoài của bức tường đó là: \(15000.\frac{{176}}{3} = 880000\)(đồng)
(Trả lời bởi Nguyễn Quốc Đạt)
Cho khối tròn xoay như Hình 39.
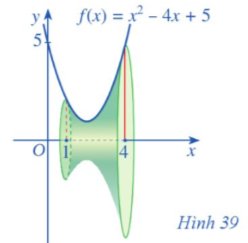
a) Hình phẳng được giới hạn bởi các đường nào để khi quay quanh trục Ox ta được khối tròn xoay như Hình 39?
b) Tính thể tích khối tròn xoay đó.
Thảo luận (1)Hướng dẫn giảia) Hình phẳng được giới hạn bởi đồ thị hàm số \(f(x) = {x^2} - 4x + 5\), trục Ox, hai đường thẳng x = 1 và x = 4 để khi quay quanh trục Ox ta được khối tròn xoay như Hình 39.
b) Thể tích khối tròn xoay đó là: \(V = \pi \int\limits_1^4 {{f^2}(x)} dx = \int\limits_1^4 {{{\left( {{x^2} - 4x + 5} \right)}^2}dx} = \frac{{78}}{5}\pi\).
(Trả lời bởi Nguyễn Quốc Đạt)
Biết F(x) = x3 là một nguyên hàm của hàm số f(x) trên ℝ. Giá trị của \(\int\limits^2_1\left[2+f\left(x\right)\right]dx\) bằng:
A. \(\dfrac{23}{4}\). B. 7. C. 9. D. \(\dfrac{15}{4}\).
Thảo luận (1)Hướng dẫn giải\(\int\limits_1^2 {[2 + f(x)]dx} = \int\limits_1^2 {2dx} + \int\limits_1^2 {f(x)dx} = \left. {2x} \right|_1^2 + \left. {{x^3}} \right|_1^2 = 9\)
Chọn C
(Trả lời bởi Nguyễn Quốc Đạt)
Biết \(\int\limits^1_0\left[f\left(x\right)+2x\right]dx=2\). Khi đó, \(\int\limits^1_0f\left(x\right)dx\) bằng:
A. 1. B. 4. C. 2. D. 0.
Thảo luận (1)Hướng dẫn giải\(\int\limits_0^1 {[f(x) + 2x]dx} = \int\limits_0^1 {f(x)dx} + \int\limits_0^1 {2xdx} = \int\limits_0^1 {f(x)dx} + \left. {{x^2}} \right|_0^1 = 2 \Leftrightarrow \int\limits_0^1 {f(x)dx} = 1\)
Chọn A
(Trả lời bởi Nguyễn Quốc Đạt)
Tìm:
a) \(\int2x\left(x^3-x+2\right)dx\); b) \(\int\left(2x+\dfrac{1}{x^3}\right)dx\); c) \(\int\left(3+2\tan^2x\right)dx\);
d) \(\int\left(1-3\cot^2x\right)dx\); e) \(\int\left(\sin x+2^{-x+1}\right)dx\); g) \(\int\left(2.6^{2x}-e^{-x+1}\right)dx\).
Thảo luận (1)Hướng dẫn giảia) \(\int {2x({x^3}} - x + 2)dx = \int {\left( {2{x^4} - 2{x^2} + 4x} \right)} dx = \frac{2{{x^5}}}{5} - \frac{{2{x^3}}}{3} + 2{x^2} + C\)
b) \(\int {\left( {2x + \frac{1}{{{x^3}}}} \right)} dx = {x^2} - \frac{1}{{2{x^2}}} + C\)
c) \(\int {\left( {3 + 2{{\tan }^2}x} \right)} dx = \int {\left( {1 + 2(1 + {{\tan }^2}x)} \right)} dx = \int {(1 + } \frac{2}{{{{\cos }^2}x}})dx = x + 2\tan x + C\)
d) \(\int {\left( {1 - 3{{\cot }^2}x} \right)} dx = \int {(4 - 3(1 + {{\cot }^2}} x))dx = \int {\left( {4 - \frac{3}{{{{\sin }^2}x}}} \right)dx = 4x + 3\cot x + C} \)
e) \(\int {\left( {\sin + {2^{ - x + 1}}} \right)} dx = - \cos x - \frac{{{2^{ - x + 1}}}}{{\ln 2}} + C\)
g) \(\int {\left( {{{2.6}^{2x}} - {e^{ - x + 1}}} \right)} dx = \frac{{{6^{2x}}}}{{\ln 6}} - {e^{ - x + 1}} + C\)
(Trả lời bởi Nguyễn Quốc Đạt)
a) Cho hàm số f(x) = x2 + e– x. Tìm nguyên hàm F(x) của hàm số f(x) trên ℝ sao cho F(0) = 2 023.
b) Cho hàm số g(x) = \(\dfrac{1}{x}\) (x > 0). Tìm nguyên hàm G(x) của hàm số g(x) trên khoảng (0; + ∞) sao cho G(1) = 2 023.
Thảo luận (1)Hướng dẫn giảia) \(F(x) = \int {f(x)} = \int {\left( {{x^2} + {e^{ - x}}} \right)dx} = \frac{{{x^3}}}{3} - {e^{ - x}} + C\)
F(0) = 2023 => C = 2024
Vậy \(F(x) = \frac{{{x^3}}}{3} - {e^{ - x}} + 2024\)
b) \(\int {g(x)} = \int {\frac{1}{x}dx} = \ln x + C\)
G(1) = 2023 => C = 2022
Vậy \(G(x) = \ln x + 2023\)
(Trả lời bởi Nguyễn Quốc Đạt)
Tính:
a) \(\int\limits^1_{-1}\left(x+2\right)^3dx\); b) \(\int\limits^2_1\dfrac{2}{x^2}dx\); c) \(\int\limits^4_1x^2\sqrt{x}dx\);
d) \(\int\limits^0_{-1}2^{3x+2}dx\); e) \(\int\limits^2_02^x.3^{x+1}dx\); g) \(\int\limits^1_0\dfrac{7^x}{11^x}dx\).
Thảo luận (1)Hướng dẫn giảia) \(\int\limits_{ - 1}^1 {{{(x + 2)}^3}} dx = \left. {\frac{{{{(x + 2)}^4}}}{4}} \right|_{ - 1}^1 = 20\)
b) \(\int\limits_1^2 {\frac{2}{{{x^2}}}} dx = \left. { - \frac{2}{x}} \right|_1^2 = 1\)
c) \(\int\limits_1^4 {{x^2}\sqrt x } dx = \int\limits_1^4 {{x^{\frac{5}{2}}}} dx = \left. {\frac{2}{7}{x^{\frac{7}{2}}}} \right|_1^4 = \frac{{254}}{7}\)
d) \(\int\limits_{ - 1}^0 {{2^{3x + 2}}} dx = \left. {\frac{{{2^{3x + 2}}}}{{3.\ln 2}}} \right|_{ - 1}^0 = \frac{4}{{3\ln 2}} - \frac{1}{{6\ln 2}}\)
e) \(\int\limits_0^2 {{2^x}{{.3}^{x + 1}}} dx = \int\limits_0^2 {{6^x}.3} dx = \left. {\frac{{{{3.6}^x}}}{{\ln 6}}} \right|_0^2 = \frac{{105}}{{\ln 6}}\)
g) \(\int\limits_0^1 {\frac{{{7^x}}}{{{{11}^x}}}} dx = \left. {\frac{{{{\left( {\frac{7}{{11}}} \right)}^x}}}{{\ln \frac{7}{{11}}}}} \right|_0^1 = \frac{{ - 4}}{{11\ln \frac{7}{{11}}}}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Một khinh khí cầu bay với độ cao (so với mực nước biển) tại thời điểm t là h(t), trong đó t tính bằng phút, h(t) tính bằng mét. Tốc độ bay của khinh khí cầu được cho bởi hàm số
v(t) = – 0,12t2 + 1,2t,
với t tính bằng phút, v(t) tính bằng mét/phút. Tại thời điểm xuất phát (t = 0), khinh khí cầu ở độ cao 520 m và 5 phút sau khi xuất phát, khinh khí cầu đã ở độ cao 530 m.
(Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma-1, Cornelsen 2016)
a) Viết công thức xác định hàm số h(t) (0 ≤ t ≤ 29).
b) Độ cao tối đa của khinh khí cầu khi bay là bao nhiêu?
c) Khi nào khinh khí cầu sẽ trở lại độ cao khi xuất phát?
Thảo luận (1)Hướng dẫn giảia) \(h(t) = \int {v(t)} dt = \int {\left( { - 0,12{t^2} + 1,2t} \right)dt} = - 0,04{t^3} + 0,6{t^2} + C\)
Tại t = 0 thì h(0) = 520 => C = 520
Vậy \(h(t) = - 0,04{t^3} + 0,6{t^2} + 520\)
b) Xét \(h(t) = - 0,04{t^3} + 0,6{t^2} + 520\)
\(h'(t) = v(t) = - 0,12{t^2} + 1,2t \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 10\end{array} \right.\)
Bảng biến thiên:

Từ bảng biến thiên, ta thấy độ cao tối đa của khinh khí cầu khi bay là 540m
c) Khinh khí cầu trở lại độ cao xuất phát khi:
\(h(t) = - 0,04{t^3} + 0,6{t^2} + 520 = 520 \Leftrightarrow \left[ \begin{array}{l}t = 0\\t = 15\end{array} \right.\)
Vậy sau 15 phút thì khinh khí cầu trở lại độ cao xuất phát
(Trả lời bởi Nguyễn Quốc Đạt)