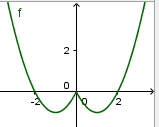
Tập hợp các điểm cực trị của hàm số \(y=x^2-2\left|x\right|\) là
\(\left\{-1;0;1\right\}\). \(\left\{0;1\right\}\). \(\left\{0\right\}\). \(\left\{-1;1\right\}\). Hướng dẫn giải:Vì hàm chẵn nên chỉ cần xét \(x\ge0\) rồi suy ra trường hợp \(x\le0\).
Với \(x\ge0\) thì \(y=x^2-2x\) là Parabol có đỉnh có hoành độ \(x_Đ=1>0\) là điểm cực trị.
Vậy với \(x\le0\) thì hàm số có thêm điểm cực trị đối xứng.
Thêm nữa đò thị cắt trục tung tại điểm (0;0) và là điểm cực trị thứ ba của hàm số (xem đồ thị).