Một người đi xe máy từ nhà (vị trí A) đến nơi làm việc (vị trí C). Do cần phải đổ xăng nên người đó đi tới trạm xăng (vị trí B) rồi mới đến nơi làm việc. Biết khoảng cách từ nhà đến trạm xăng là 1 km, và từ trạm xăng tới nơi làm việc là 1 km. Vị trí của nhà, trạm xăng và nơi làm việc được biểu diễn trên hình vẽ. Tính quãng đường người đó đã đi và độ dịch chuyển của người đó.
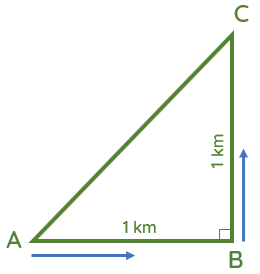
Quãng đường đi được của người đó là: \(s=\) km
Vì tam giác ABC là tam giác vuông, nên độ lớn của độ dịch chuyển \(\overrightarrow{AC}\) của người đó là:
\(d=AC=\sqrt{AB^2+BC^2}\simeq\) 1,4 km (kết quả là số thập phân có 1 chữ số sau dấu phẩy)
Vì tam giác ABC là tam giác vuông cân nên \(\widehat{CAB}=45^o\)
Vậy độ dịch chuyển của người đó là \(d=\) km (hướng \(45^o\) Đông - Bắc || Tây - Nam || Đông - Nam)

