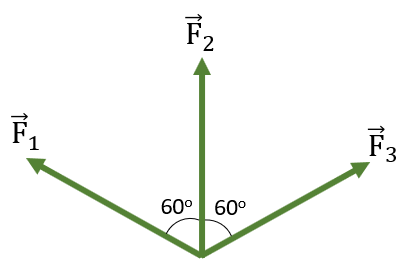
Một chất điểm chịu tác dụng của ba lực \(\overrightarrow{F_1}\), \(\overrightarrow{F_2}\), \(\overrightarrow{F_3}\) có cùng độ lớn \(10\) N. Biết góc tạo bởi các lực \(\left(\overrightarrow{F_1},\overrightarrow{F_2}\right)=\left(\overrightarrow{F_2},\overrightarrow{F_3}\right)=60^o\). Hợp lực của ba lực này có độ lớn là
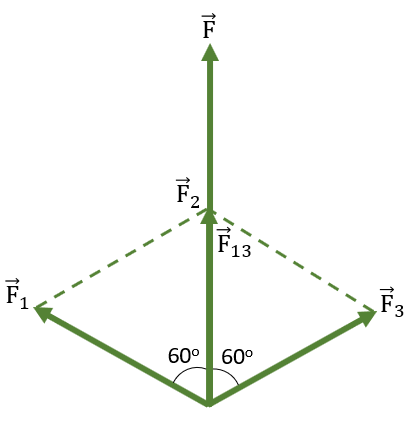
Hợp lực: \(\overrightarrow{F}=\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}=\overrightarrow{F_{13}}+\overrightarrow{F_2}\)
\(F_{13}=\sqrt{F_1^2+F_3^2+2F_1F_3.cos120^o}\) \(=\sqrt{10^2+10^2+2.10.10.cos120^o}=10\) N
Theo quy tắc hình bình hành, kết hợp với điều kiện ba lực \(\overrightarrow{F_1}\), \(\overrightarrow{F_2}\), \(\overrightarrow{F_3}\) có cùng độ lớn, do đó hình bình hành thành hình thoi. Vậy hợp lực \(\overrightarrow{F_{13}}\) của lực \(\overrightarrow{F_1}\) và \(\overrightarrow{F_3}\) có cùng phương, cùng chiều và cùng độ lớn với lực \(\overrightarrow{F_2}\).
Khi đó ta có: \(F=F_{13}+F_2=10+10=20\) N.

