Cho tam giác \(ABC\) có \(AB=6cm;AC=8cm;BC=10cm.\) Gọi \(M\) là trung điểm \(BC\). Kẻ \(MN\) vuông góc \(AB\). Độ dài \(MN\) là
\(3cm.\)\(4cm.\)\(5cm.\)\(6cm.\)Hướng dẫn giải: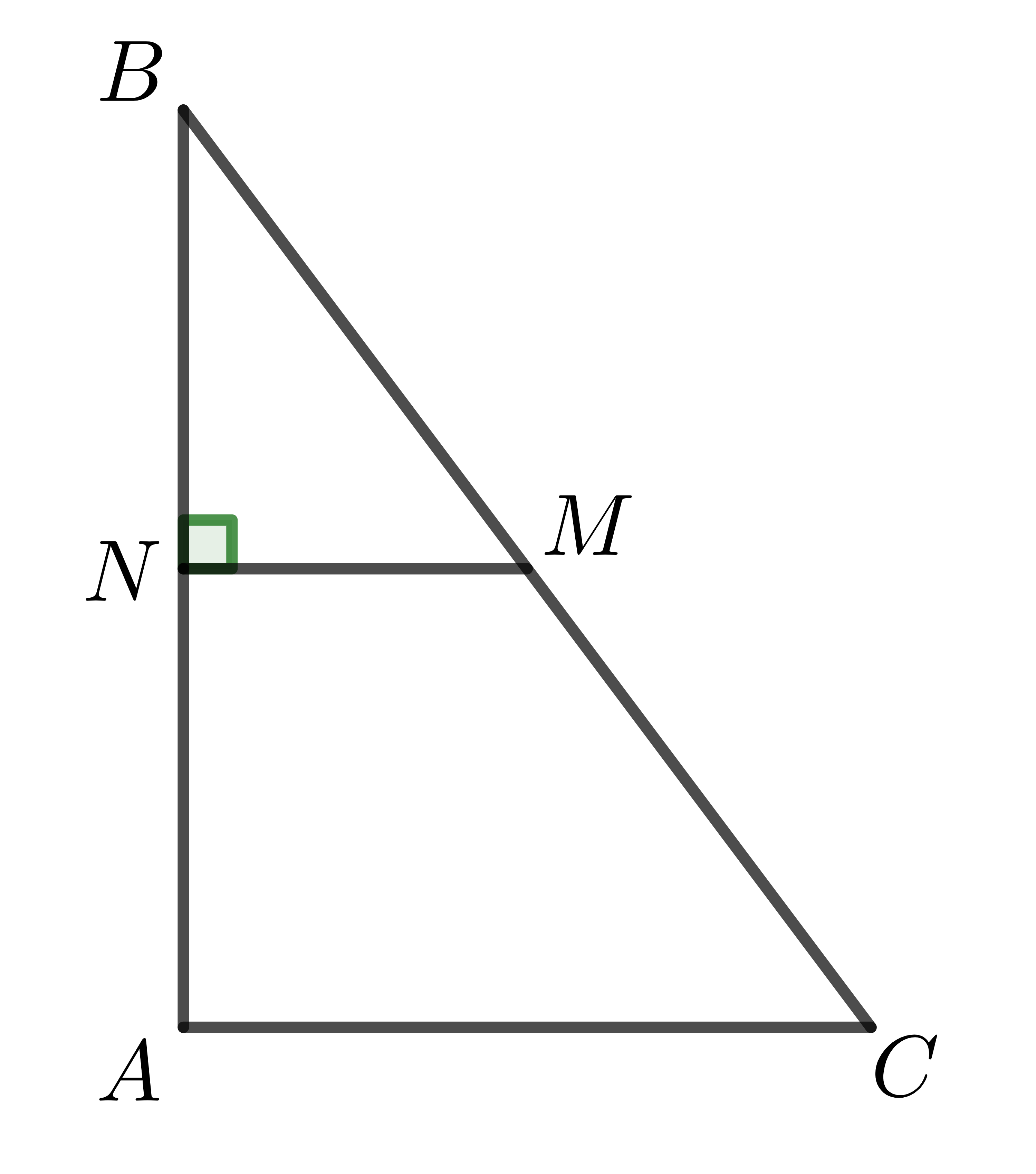
Ta có \(AB^2+AC^2=6^2+8^2=100=BC^2\). Theo định lí Pytago đảo ta có \(\Delta ABC\) vuông tại \(A\)
\(\Rightarrow AB\perp AC\) mà \(MN\perp AB\) \(\Rightarrow MN\)//\(AC\).
Mặt khác \(M\) là trung điểm \(AC\) \(\Rightarrow MN\) là đường trung bình của tam giác \(ABC\)
\(\Rightarrow MN=\dfrac{1}{2}AC=\dfrac{1}{2}.8=4\left(cm\right)\).

