Cho lục giác đều ABCDEF, độ dài mỗi cạnh là a. Các đường thẳng AB và CD cắt nhau tại M,
cắt đường thẳng EF theo thứ tự tại N và P. Ta tính được bán kính đường tròn ngoại tiếp tam giác MNP là
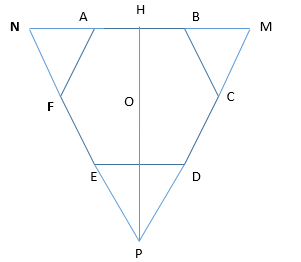
Ta dễ chứng minh được tam giác MNP đều.
Độ dài cạnh tam giác MNP là 3.a = 3a.
Kẻ PH vuông góc với MN.
Suy ra H là trung điểm của MN.
\(NH=HM=\dfrac{3a}{2}\).
Áp dụng định lý Pi-ta-go trong tam giác PHM ta có:
\(PH=\sqrt{\left(3a\right)^2-\left(\dfrac{3a}{2}\right)^2}=\dfrac{3\sqrt{3}}{2}a\).
Gọi O là tâm đường tròn nội tiếp tam giác MNP.
Ta có: \(R=\dfrac{2}{3}PH=\dfrac{2}{3}.\dfrac{3\sqrt{3}}{2}a=\sqrt{3}a\).

