Cho hình bình hành \(ABCD\) có \(AB=2.AD\). Gọi \(E,F\) lần lượt là trung điểm \(AB,CD\). Gọi \(AF\) cắt \(DE\) tại \(I\), \(BF\) cắt \(CE\) tại \(K\). Tứ giác \(EIFK\) là
Hình chữ nhật.Hình vuông.Hình thoi.Cả 3 đáp án trên đều sai.Hướng dẫn giải: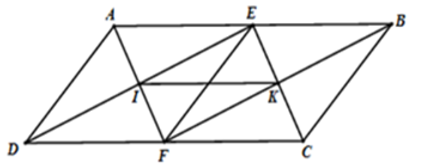
Ta dễ dàng chứng minh được \(BEDF\) là hình bình hành (\(BE\) song song và bằng \(DF\))
\(\Rightarrow BF,DE\) song song và bằng nhau.
Mặt khác, \(AEFD,BEFC\) là các hình bình hành (hai cạnh đối song song và bằng nhau) \(\Rightarrow I,K\) là trung điểm \(DE,BF\).
Như vậy \(EI,FK\) song song và bằng nhau nên \(EIFK\) là hình bình hành.
Lại có \(AE=AD\) nên \(AEFD\) là hình thoi, suy ra \(AI\perp DE\Rightarrow\widehat{EIF}=90^0\). Do đó \(EIFK\) là hình chữ nhật.

