Cho hàm số \(y=f\left(x\right)\), biết \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=+\infty;\lim\limits_{x\rightarrow-\infty}f\left(x\right)=-\infty\).
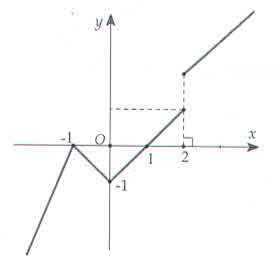
Có bao nhiêu điểm mà tại đấy hàm số không có đạo hàm?
1.2.3.4.Hướng dẫn giải:Từ đồ thị suy ra hàm đã cho gián đoạn tại x = 2 nên hàm số cũng không có đạo hàm tại điểm này.
Tại \(x=-1\) đạo hàm trái dương, đạo hàm phải âm. Do đó hàm số không có đạo hàm tại \(x=-1\)
Tại \(x=0\) đạo hàm trái âm, đạo hàm phải dương; hàm số không có đạo hàm tại \(x=0\).
Tại các điểm khác, đạo hàm tồn tại.
Đáp số: 3

