Cho đường cong (H) : \(y=\sqrt{x^2-9},\left(x\ge3\right)\) và đường thẳng (d) : \(5x-4y+30=0\). Trên (H) tồn tại một điểm M sao cho khoảng cách từ M đến (d) là ngắn nhất. Hãy xác định tọa độ điểm đó.
(5; -4) (4;-5) (5;4) (4;5)Hướng dẫn giải:
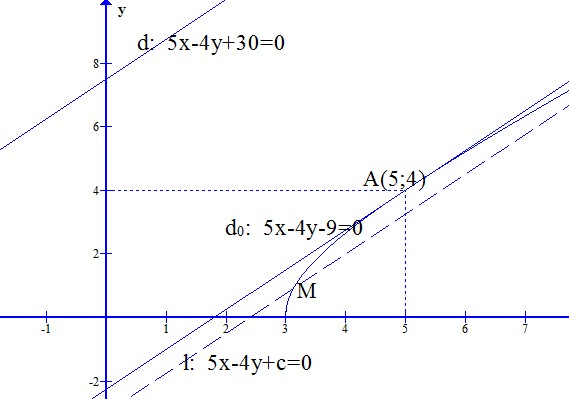
Xét một điểm M tùy ý trên đường cong đã cho. Qua M kẻ đường thẳng l song song với đường thẳng d đã cho. Khoảng cách từ M tới d cũng là khoảng cách giữa hai đường thẳng song song d và l. Bài toán trở thành: trong các cát tuyến l song song với d, hãy tìm cát tuyến gần d nhất. Ta thấy khi l trùng với tiếp tuyến (của đường cong đã cho) song song với d thì l gần d nhất. Vậy bài toán trở thành: Tìm tiếp điểm của tiếp tuyến song song với d. Các học sinh lớp 12 có thể giải bài toán này bằng đạo hàm, còn với học sinh lớp 10 thì bài toán có thể giải được nếu học sinh "nhìn thấy" đường cong đã cho là một phần của hypebol. Ta có: với điều kiện \(y\ge0,x\ge3\) thì
\(y=\sqrt{x^2-9}\Leftrightarrow y^2=x^2-9\Leftrightarrow x^2-y^2=9\Leftrightarrow\dfrac{x^2}{9}-\dfrac{y^2}{9}=1\)
nghĩa là đường cong đã cho là phần của đường hypebol \(\dfrac{x^2}{9}-\dfrac{y^2}{9}=1\) trong góc phần tư thứ nhất.
Đường thẳng \(l:5x-4y+c=0\) sẽ tiếp xúc với hypebol khi và chỉ khi \(5^2.9-\left(-4\right)^2.9=c^2\)\(\Leftrightarrow c^2=81\)\(\Leftrightarrow c=\pm9\). Nếu \(c=9\) thì \(l:5x-4y+9=0\) nên \(y=\dfrac{5x+9}{4}\), thế vào \(\dfrac{x^2}{9}-\dfrac{y^2}{9}=1\) (1) ta được
\(x^2-\left(\dfrac{5x+9}{4}\right)^2=9\Leftrightarrow9x^2+90x+16.9+81=0\) có \(\Delta'=45^2-9.9.25=45^2-\left(9.5\right)^2=0\) , phương trình có nghiệm kép \(x=-\dfrac{45}{9}=-5\), điểm M có tọa độ âm, loại.
Nếu \(c=-9\) thì \(l:5x-4y-9=0\) nên \(y=\dfrac{5x-9}{4}\), thế vào \(\dfrac{x^2}{9}-\dfrac{y^2}{9}=1\) ta được
\(x^2-\left(\dfrac{5x-9}{4}\right)^2=9\)\(\Leftrightarrow9x^2-90x+16.9+81=0\) có \(\Delta'=0\), phương trình có nghiệm kép \(x=5\), thế trở lại (1) ta được \(y=\pm4\). Do chỉ xét trong góc phần tư thứ nhất ta lấy điểm \(\left(x=5;y=4\right)\).
Đáp số: \(\left(5;4\right)\).

