MỘT SỐ HỆ THỨC VỀ CẠNH VÀ GÓC TRONG TAM GIÁC VUÔNG

1. Các hệ thức

* Định lí: Trong tam giác vuông, mỗi cạnh góc vuông bằng:

- Cạnh huyền nhân với sin góc đối hoặc nhân với côsin góc kề

- Cạnh góc vuông kia nhân với tang góc đối hoặc nhân với côtang góc kề.

* Hệ thức: 

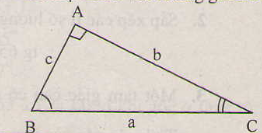
b = a.sin B = a.cos C = c.tan B = c.cot C

c = a.sin C = a.cos B = b.tan C = b.cot B

2. Áp dụng giải tam giác vuông

* Trong một tam giác vuông, nếu cho biết trước hai cạnh hoặc một cạnh và một góc nhọn thì ta sẽ tìm được tất cả các cạnh và góc còn lại của nó. Bài toán đặt ra như thế gọi là bài toán "Giải tam giác vuông".

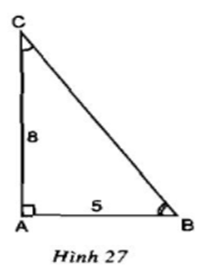
Ví dụ: Cho tam giác vuông ABC với các cạnh góc vuông AB = 5, AC = 8. Hãy giải tam giác vuông ABC.​

* Giải:

Theo định lí Py-ta-go ta có: 

\(BC=\sqrt{AB^2+AC^2}=\sqrt{5^2+8^2}\approx9,434\)

Mặt khác: 

\(tanC=\dfrac{AB}{AC}=\dfrac{5}{8}=0,625\)

Dùng máy tính bỏ túi hoặc tra bảng lượng giác ta tìm được \(\widehat{C}\approx32^o\) 

\(\Rightarrow\widehat{B}\approx90^o-32^o=58^o\)

 * Câu hỏi bổ sung: Trong ví dụ trên, hãy tính cạnh BC mà không áp dụng định lí Py-ta-go.

* Giải:

Theo ví dụ trên ta tìm được \(\widehat{C}\approx32^o\)

Xét tam giác ABC vuông tại A, theo hệ thức về cạnh và góc trong tam giác vuông ta có:

\(AB=BC.sinC\)

\(\Rightarrow\) \(BC=\dfrac{AB}{sinC}\approx\dfrac{5}{sin32^o}\approx9,435\)

Vậy BC \(\approx\) 9,435.