Bài 2. Phương trình trạng thái khí lí tưởng

I. MỐI LIÊN HỆ GIỮA THỂ TÍCH VÀ ÁP SUẤT CHẤT KHÍ

Xét bình kín chứa một lượng khí xác định. Các thông số của lượng khí mà chúng ta có thể đo được là áp suất, nhiệt độ và thể tích. Chúng được gọi là các thông số trạng thái của chất khí.

1. Khảo sát mối liên hệ giữa thể tích và áp suất của chất khí khi nhiệt độ không đổi

Có thể rút ra mối liên hệ giữa thể tích và áp suất của một lượng khí xác định khi giữ nhiệt độ của lượng khí không đổi bằng thí nghiệm sau đây.

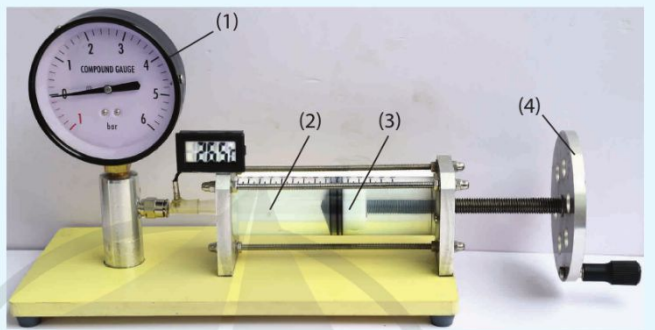
2. Định luật Boyle

Thí nghiệm trên cho thấy mối liên hệ giữa áp suất \(p\) và thể tích \(V\) của một lượng khí : khi bị nén thể tích của nó giảm, áp suất tăng lên và ngược lại. Đây là nội dung định luật được nhà khoa học người Ireland là Robert Boyle (Rô-bớt Bôi-lơ) phát biểu vào năm 1662 :

Với một khối lượng khí xác định, khi giữ nhiệt độ của khí không đổi thì áp suất gây ra bởi khí tỉ lệ nghịch với thể tích của nó.

Quá trình biến đổi trạng thái trong đó nhiệt độ được giữ không đổi được gọi là quá trình đẳng nhiệt. Công thức của định luật Boyle được viết dưới dạng :

\(pV=\) hằng số

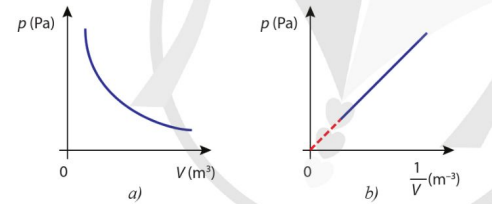
Hình 2.4 là đồ thị biểu diễn định luật Boyle. Trong đó, Hình 2.4b là đồ thị của \(p\) theo \(\dfrac{1}{V}\) , có dạng đường thẳng mà nếu kéo dài sẽ đi qua gốc tọa độ.

Công thức \(pV=\) hằng số thường được viết dưới dạng :

\(p_1V_1=p_2V_2\)

Trong đó, \(p_1\) và \(V_1\), \(p_2\) và \(V_2\) lần lượt là áp suất và thể tích của khí ứng với hai trạng thái khác nhau.

Ví dụ

Một lượng khí ở nhiệt độ 18 \(^oC\) có thể tích 1 m³ và áp suất 1 atm. Người ta nén đẳng nhiệt lượng khí này đến áp suất 3,5 atm. Xác định thể tích khí sau khi nén.

Giải

Xác định các thông số áp suất và thể tích của hai trạng thái :

Trạng thái 1 : \(p_1\) = 1 atm, \(V_1\) = 1 m³

Trạng thái 2 : \(p_2\) = 3,5 atm, \(V_2\) = ?.

Quá trình nén khí là đẳng nhiệt nên theo định luật Boyle, ta có :

\(p_1V_1=p_2V_2\)

\(\Leftrightarrow V_2=\dfrac{p_1V_1}{p_2}=\dfrac{1.1}{3,5}=0,3\) m³

II. MỐI LIÊN HỆ GIỮA THỂ TÍCH VÀ NHIỆT ĐỘ CỦA CHẤT KHÍ

1. Định luật Charles

Từ giữa thế kỉ XVII, Boyle đã nghiên cứu sự thay đổi các thông số trạng thái của một lượng khí xác định khi giữ nhiệt độ của khí không đổi. Nhưng phải hơn một thế kỉ sau mới có những kết quả mới từ các thí nghiệm về chất khí. Jaques Charles (Giắc-kê Sác-lơ), từ năm 1787, đã tiến hành thí nghiệm với các khí khác nhau được giữ ở áp suất không đổi. Quá trình thay đổi trạng thái của một lượng khí xác định mà áp suất khí không đổi được gọi là quá trình đẳng áp. Hình 2.5 thể hiện kết quả các thí nghiệm khảo sát của Charles về mối liên hệ giữa thể tích và nhiệt độ của một lượng khí khi áp suất không đổi.

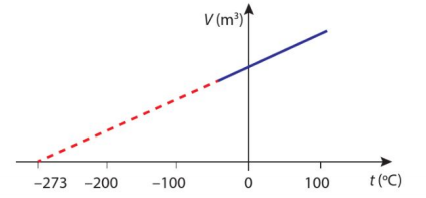
Mối liên hệ giữa thể tích \(V\) và nhiệt độ \(T\) trong quá trình đẳng áp được biểu diễn bằng công thức :

\(\dfrac{V}{T}\)= hằng số

Định luật Charles được phát biểu như sau :

Với một khối lượng khí xác định, khi giữ ở áp suất không đổi thì thể tích của khí tỉ lệ thuận với nhiệt độ tuyệt đối của nó.

2. Thí nghiệm minh họa

Có thể minh họa mối liên hệ giữa nhiệt độ và thể tích của một lượng khí xác định khi giữ áp suất của khí không đổi bằng thí nghiệm sau đây.

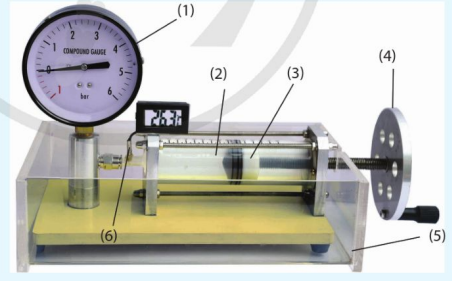
III. PHƯƠNG TRÌNH TRẠNG THÁI KHÍ LÍ TƯỞNG

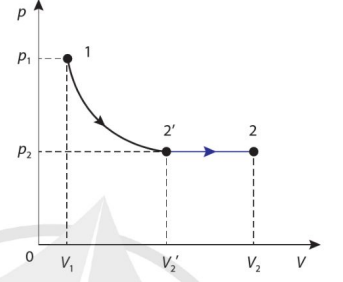
Xét một lượng khí xác định chuyển từ trạng thái 1 có các giá trị nhiệt độ, thể tích và áp suất lần lượt là \(T_1\), \(V_1\) và \(p_1\) sang trạng thái 2 có các giá trị nhiệt độ, thể tích và áp suất lần lượt là \(T_2\), \(V_2\) và \(p_2\). Để tìm mối liên hệ giữa các giá trị này, ta thực hiện quá trình biến đổi của lượng khí từ trạng thái 1 sang trạng thái 2 theo hai giai đoạn.

Đầu tiên, cho lượng khí thực hiện quá trình đẳng nhiệt 1 → 2'.

Tiếp theo, cho lượng khí thực hiện quá trình đẳng áp 2' → 2         (Hình 2.9).

Áp dụng công thức \(pV=\) hằng số cho quá trình đẳng nhiệt 1 → 2', ta có :

         \(p_1V_1=p_2V'_2\)

Áp dụng công thức \(\dfrac{V}{T}\) = hằng số cho quá trình đẳng áp 2' → 2, ta có :

         \(\dfrac{V'_2}{T_1}=\dfrac{V_2}{T_2}\)

Từ \(p_1V_1=p_2V'_2\) và \(\dfrac{V'_2}{T_1}=\dfrac{V_2}{T_2}\)  , ta có :

         \(\dfrac{p_1V_1}{T_1}=\dfrac{p_2V_2}{T_2}\)

Vì việc chọn các trạng thái 1, 2 là bất kì nên ta có :

          \(\dfrac{pV}{T}\)= hằng số

Để tìm mối liên hệ giữa các thông số trạng thái của chất khí khi xét các lượng khí khác nhau, ta giả sử giữ cho nhiệt độ và áp suất của các lượng khí đó không đổi. Khi đó, thể tích sẽ tỉ lệ thuận với khối lượng khí. Nói cách khác, hằng số trong phương trình tỉ lệ thuận với khối lượng khí đang xét.

Biết khối lượng khí đag xét thì ta có thể tính số mol khí theo công thức:

           \(n=\dfrac{m}{M}\)

trong đó, \(m\) là khối lượng khí và \(M\) là khối lượng mol nguyên tử hoặc phân tử của chất khí đó. Như vậy, ta có thể viết lại phương trình \(\dfrac{pV}{T}\)= hằng số dưới dạng :

\(pV=nRT\)

với \(n\) là số mol khí đang xét và \(R\) là một hằng số có giá trị thực nghiệm là : R = 8,31 J/(mol.K). R được gọi là hằng số khí lí tưởng.

Phương trình \(pV=nRT\) được gọi là phương trình trạng thái của khí lí tưởng.

Các chất khí trong thực tế như oxygen, nitrogen, carbon dioxide,... (còn được gọi là khí thực) chỉ tuân theo các định luật Boyle, Charles ở các điều kiện nhiệt độ và áp suất thông thường nên phương trình \(pV=nRT\) chỉ gần đúng với các khí thực. Tuy nhiên, ở áp suất không quá cao và nhiệt độ không quá thấp, ta có thể áp dụng phương trình trạng thái của khí lí tưởng để tính áp suất, thể tích và nhiệt độ của khí thực.