Đây là phiên bản do Nguyễn Phương Mai
đóng góp và sửa đổi vào 25 tháng 12 2021 lúc 7:49. Xem phiên bản hiện hành
Bài 1. Tập hợp
Nội dung lý thuyết
Các phiên bản khác
0
3 gp
1. Tập hợp và phần tử của tập hợp
Một số ví dụ về tập hợp:
Tập hợp các con cá trong bình |
Tập hợp các bông hoa trong lọ hoa |
Tập hợp các con tem trong hình |
Một tập hợp (gọi tắt là tập) bao gồm những đối tượng nhất định. Chúng được gọi là những phần tử của tập hợp đó.
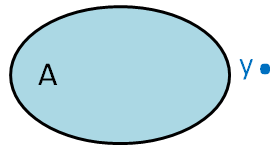
x là một phần tử của tập A,
kí hiệu là x ∈ A
(đọc là x thuộc A)
y không là phần tử của tập A, kí hiệu là y ∉ A
(đọc là y không thuộc A)
Chú ý.
- Khi x thuộc A, ta còn nói "x nằm trong A", hay "A chứa x".
- Người ta thường đặt tên tập hơp bằng chữ cái in hoa: A, B, C, D, ...
Ví dụ 1. Cho tập hợp C.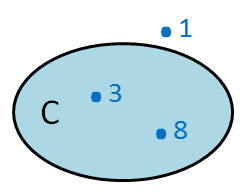
a) Tập hợp C chứa những số nào?
b) Số 1 có thuộc tập C không?
Giải:
a) Tập C chứa số 3 và số 8, kí hiệu 3 ∈ C, 8 ∈ C.
b) Số 1 không thuộc tập hợp C, kí hiệu 1 ∉ C.
Ví dụ 2. Gọi D là tập hợp các chữ cái trong từ LỚP HỌC. Khi đó H ∈ D, N ∉ D.
2. Mô tả một tập hợp
Mô tả tập hợp là cho biết cách xác định các phần tử của tập hợp đó.
Có hai cách mô tả một tập hợp:
Cách 1. Liệt kê các phần tử của tập hợp, tức là viết các phần tử trong dấu ngoặc { } theo thứ tự tùy ý nhưng mỗi phần tử chỉ được viết một lần.
Ví dụ, với tập Q gồm các số 0, 2, 4, 6, 8 ở hình bên,
ta viết: Q = {0; 2; 4; 6; 8}.
Cách 2. Nêu dấu hiệu đặc trưng cho các phần tử của tập hợp
Ví dụ, với tập Q ta cũng có thể viết:
Q = {x| x là số tự nhiên chẵn nhỏ hơn 10}.
Chú ý:
- Ta viết các phần tử của tập hợp cách nhau bởi dấu ";".
- Tập hợp các số tự nhiên kí hiệu là \(\mathbb{N}\), tức là \(\mathbb{N}\) = {0; 1; 2; 3; ...}.
- Tập hợp các số tự nhiên khác 0 kí hiệu là \(\mathbb{N^*}\), tức là \(\mathbb{N^*}\) = {1; 2; 3; 4; ...}.
Ví dụ. Viết mỗi tập hợp sau bằng cách liệt kê các phần tử của chúng:
A = {x ∈ \(\mathbb{N}\) | x < 7}; B = {x ∈ \(\mathbb{N^*}\) | x < 7}.
Giải:
A = {0; 1; 2; 3; 4; 5; 6}.
B = {1; 2; 3; 4; 5; 6}.
Danh sách các phiên bản khác của bài học này. Xem hướng dẫn




.png)