Xác định tính đúng sai của mệnh đề phủ định \(\overline{A}\) theo tính đúng sai của mệnh đề A
Ôn tập chương I
Bài 1 (SGK trang 24)
Thảo luận (1)
Bài 2 (SGK trang 24)
Thế nào là mệnh đề đảo của mệnh đề \(A\Rightarrow B\) ? Nếu \(A\Rightarrow B\) là mệnh đề đúng thì mệnh đề đảo của nó có đúng không ? Cho ví dụ minh họa ?
Thảo luận (1)Hướng dẫn giảiMệnh đề đảo của mệnh đề A ⇒ B là mệnh đề B ⇒A.
Ví dụ 1: A ⇒ B = “Nếu một số nguyên chia hết cho 3 thì nó có tổng các chữ số chia hết cho 3”. Mệnh đề này đúng.
Mệnh đề đảo: B ⇒A = “Nếu một số nguyên có tổng các chữ số chia hết cho 3 thì số đó chia hết cho 3”. Mệnh đề này cũng đúng.
Ví dụ 2: A ⇒ B = “Nếu một tứ giác là hình thoi thì nó có hai đường chéo vuông góc với nhau”. Mệnh đề này đúng.
Mệnh đề đảo: B ⇒A = “Nếu một tứ giác có hai đường chéo vuông góc với nhau thì tứ giác ấy là một hình thoi”. Mệnh đề này sai.
(Trả lời bởi Hiiiii~)
Bài 3 (SGK trang 24)
Thế nào là hai mệnh đề tương đương ?
Thảo luận (1)Hướng dẫn giảiĐịnh nghĩa.
Nếu A ⇒B là một mệnh đề đúng và mệnh đề B ⇒A cũng là mệnh đề đúng thì ta nói A tương đương với B, kí hiệu là A ⇔B
Khi A ⇔B, ta cũng nói A là điều kiện cần và đủ để có B hoặc A khi và chỉ khi B hay A nếu và chỉ nếu B.
(Trả lời bởi Hiiiii~)
Bài 4 (SGK trang 24)
Nêu định nghĩa tập hợp con của một tập hợp và định nghĩa hai tập hợp bằng nhau ?
Thảo luận (1)Hướng dẫn giảiTập hợp con: Ta gọi A là tập hợp con của B, kí hiệu A⊂B, nếu mỗi phần tử của A là một phần tử của B
A⊂B ⇔ x ∈ A ⇒ x ∈B
Hai tập hợp bằng nhau: Hai tập hợp A và B là bằng nhau, kí hiệu A = B, nếu tất cả phần tử của chúng như nhau
A = B ⇔ A⊂B và B ⊂ A
(Trả lời bởi Hiiiii~)
Bài 5 (SGK trang 24)
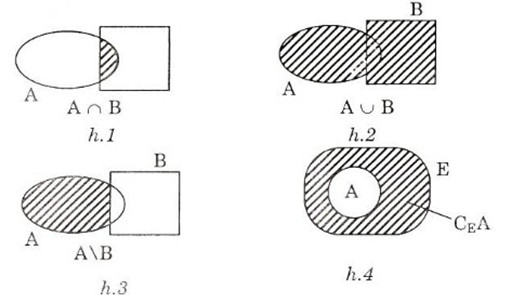
Nêu các định nghĩa hợp, giao, hiệu và phần bù của hai tập hợp. Minh họa các khái niệm bằng hình vẽ ?
Thảo luận (1)Hướng dẫn giảiA∩B ⇔ ∀x (x∈A và x∈B) (h.1)
A ∪B ⇔ ∀x (x∈A hoặc x∈B) (h.2)
A\B ⇔ ∀x (x∈A và x∉B) (h.3)
Cho A⊂E.CEA = {x/x∈E và x∉A} (h.4)
(Trả lời bởi Hiiiii~)
Bài 6 (SGK trang 24)
Nêu định nghĩa đoạn \(\left[a;b\right]\), khoảng \(\left(a;b\right)\), nửa khoảng [a;b), (a,b], (\(-\infty;b\)], [a; \(+\infty\)).
Viết tập hợp R các số thực dưới dạng 1 khoảng ?
Thảo luận (1)Hướng dẫn giảix ∈ [a;b] ⇔ a ≤ x ≤ b
x ∈ (a;b) ⇔ a < x < b
x ∈ [a;b) ⇔ a ≤ x < b
x ∈ (a,b] ⇔ a < x ≤ b
x ∈ (-∞;b] ⇔ x ≤ b
x ∈ [a, +∞) ⇔ x ≥ a
(Trả lời bởi Hiiiii~)
Bài 7 (SGK trang 24)
Thế nào là sai tuyệt đối của một số gần đúng ?
Thế nào là độ chính xác của một số gần đúng ?
Thảo luận (1)Hướng dẫn giảiNếu \(a\) là số gần đúng của số đúng \(\overline{a}\) thì \(\Delta_a=\left|\overline{a}-a\right|\) được gọi là sai số tuyệt đối của số gần đúng \(a\).
(Trả lời bởi Bùi Thị Vân)
Nếu \(\Delta_a=\left|\overline{a}-a\right|\le d\) thì \(-d\le\overline{a}-a\le d\) hay \(a-d\le\overline{a}\le a+d\) .
Ta nói \(a\) là số gần đúng của \(\overline{a}\) với độ chính xác \(d\), và quy ước viết gọn là \(\overline{a}=a\pm d\).
Bài 8 (SGK trang 24)
Cho tứ giác ABCD. Xét tính đúng sai của mệnh đề \(P\Rightarrow Q\) với :
a. P : "ABCD là một hình vuông"
Q : " ABCD là một hình bình hành"
b. P : "ABCD là một hình thoi"
Q : "ABCD là một hình chữ nhật"
Thảo luận (1)Hướng dẫn giảia) P ⇒ Q = “Nếu ABCD là một hình vuông thì nó là một hình bình hành”. Mệnh đề này đúng.
b) P ⇒ Q = “Nếu ABCD là một hình thoi thì ABCD là một hình chữ nhật. Mệnh đề này sai.
(Trả lời bởi Hiiiii~)
Bài 9 (SGK trang 25)
Xét mối quan hệ bao hàm giữa các tập hợp sau :
A là tập hợp các hình tứ giác
B là tập hợp các hình bình hành
C là tập hợp các hình thang
D là tập hợp các hình chữ nhật
E là tập hợp các hình vuông
G là tập hợp các hình thoi
Thảo luận (1)Hướng dẫn giải
Bài 10 (SGK trang 25)
Liệt kê các phần tử của mỗi tập hợp sau :
a. \(A=\) { \(3k-2\) | \(k=0,1,2,3,4,5\)}
b. \(B=\) { \(x\in N\) |\(x\le12\) }
c. \(C=\) { \(\left(-1\right)^n\) | \(n\in N\) }
Thảo luận (1)Hướng dẫn giảia) A = {-2, 1, 4, 7, 10, 13}
b) B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12}
c) C = {-1, 1}
(Trả lời bởi Hiiiii~)