Trên hình 33 hãy chỉ ra các tam giác đồng dạng. Viết các cặp tam giác đồng dạng theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng ?
Bài 8: Các trường hợp đồng dạng của tam giác vuông
Bài 47 (Sách bài tập - tập 2 - trang 95)
Thảo luận (1)
Bài 48 (Sách bài tập - tập 2 - trang 95)
Cho tam giác ABC (\(\widehat{A}=90^0\)) có đường cao AH (h.34).
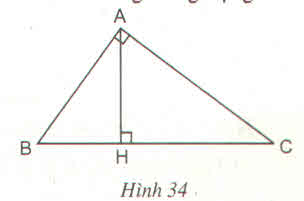
Chứng minh rằng : \(AH^2=BH.CH\)
Thảo luận (2)Hướng dẫn giảixét tam giác AHB và tam giác CHA có
góc H = 90 độ
AH là cạnh chung
góc B = góc C (kề bù)
suy ra tam giác AHB đồng dạng tam giác CHA( G.C.G)
\(\dfrac{AH}{CH}=\dfrac{HB}{AH}\Rightarrow AH\cdot AH=HB\cdot HC\)
\(\Rightarrow AH^2=HB\cdot HC\)
(Trả lời bởi Nguoi Ay)
Bài 49 (Sách bài tập - tập 2 - trang 96)
Đường cao của một tam giác vuông xuất phát từ đỉnh góc vuông chia cạnh huyền thành hai đoạn thẳng có độ dài là 9cm và 16 cm.
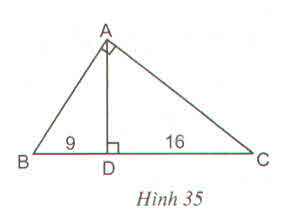
Tính độ dài các cạnh của tam giác vuông đó (h.35) ?
Thảo luận (3)Hướng dẫn giải\(AB^2 + AC^2 = 25^2 = 625\)
\(AD^2 + 81 = AB^2\)
\(AD^2 + 256 = AC^2\)
\(=> AD^2 + 81 + AD^2 + 256 = 625\)
=> \(2AD^2 = 288\)
=> \(AD^2 = 144\)
=> AD = 12(cm)
=>\( AB^2 = 9^2 + 12^2 = 225\)
=> AB = 15 (cm)
=> \(AC^2 = 12^2 + 16^2 = 400\)
=> AC = 20(cm)
và BC = 25(cm)
(Trả lời bởi Trần Đăng Nhất)
Bài 50 (Sách bài tập - tập 2 - trang 96)
Tam giác vuông ABC (\(\widehat{A}=90^0\)) có đường cao AH và trung tuyến AM (h.36).
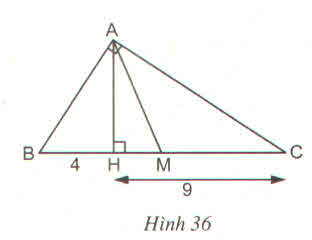
Tính diện tích tam giác AMH, biết BH = 4cm, CH = 9cm ?
Thảo luận (2)Hướng dẫn giải
Bài 8.1 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 96)
Cho góc nhọn xOy. Trên tia Ox lấy một điểm A sao cho OA 8,65cm. Trên tia Oy lấy một điểm B sao cho OB 15,45 cm. Vẽ AE vuông góc với Oy, BF vuông góc với Ox. Biết độ dài đoạn thẳng BF 10,25 cm
Độ dài của đoạn thẳng AE (lấy chính xác đến hai chữ số thập phân) là :
(A) 13,04cm (B) 18,31cm
(C) 5,74cm (D) 5,73cm
Hãy chọn kết quả đúng ?
Đọc tiếp
Cho góc nhọn xOy. Trên tia Ox lấy một điểm A sao cho OA = 8,65cm. Trên tia Oy lấy một điểm B sao cho OB = 15,45 cm. Vẽ AE vuông góc với Oy, BF vuông góc với Ox. Biết độ dài đoạn thẳng BF = 10,25 cm
Độ dài của đoạn thẳng AE (lấy chính xác đến hai chữ số thập phân) là :
(A) 13,04cm (B) 18,31cm
(C) 5,74cm (D) 5,73cm
Hãy chọn kết quả đúng ?
Thảo luận (1)Hướng dẫn giải
Bài 8.2 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 96)
Tam giác ABC vuông tại A có đường cao AH = n = 10,85cm và cạnh AB = m = 12,5cm. Hãy tính độ dài các cạnh còn lại của tam giác (chính xác đến hai chữ số thập phân)
Thảo luận (1)Hướng dẫn giải
Bài 8.3 - Bài tập bổ sung (Sách bài tập - tập 2 - trang 96)
Cho tam giác ABC vuông tại A, chân H của đường cao AH chia cạnh huyền BC thành hai đoạn có độ dài 4cm và 9 cm
Gọi D và E là hình chiếu của H trên AB và AC
a) Tính độ dài DE
b) Các đường thẳng vuông góc với DE tại D và E cắt BC theo thứ tự tại M và N. Chứng minh M là trung điểm của BF, N là trung điểm của CH
c) Tính diện tích tứ giác DENM
Thảo luận (1)Hướng dẫn giải
