Hình 65 mô tả một chiếc quạt giấy.
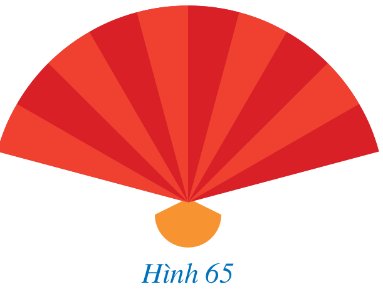
Hình phẳng được tô màu đỏ ở Hình 65 được gọi là hình gì và diện tích của hình đó được tính như thế nào?
Hình 65 mô tả một chiếc quạt giấy.

Hình phẳng được tô màu đỏ ở Hình 65 được gọi là hình gì và diện tích của hình đó được tính như thế nào?
Lấy một vòng tròn không dãn có dạng hình tròn (Hình 66a), cắt vòng dây và kéo thẳng vòng dây đó để nhận được sợi dây như ở Hình 66b.
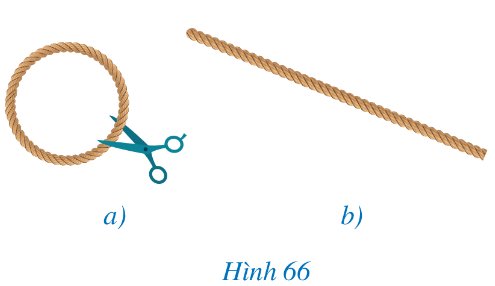
Đo chiều dài sợi dây đó.
Ta nói chiều dài sợi dây bằng chu vi của đường tròn.
Thảo luận (1)Hướng dẫn giảiHọc sinh tự thực hiện theo yêu cầu.
(Trả lời bởi Nguyễn Quốc Đạt)
Tính chu vi của đường tròn bán kính 5 cm theo đơn vị centimét.
Thảo luận (1)Hướng dẫn giảiChu vi của đường tròn là:
\(C = 2\pi R = 2\pi .5 = 10\pi \approx 31,4\left( {cm} \right)\).
(Trả lời bởi Nguyễn Quốc Đạt)
a) Đánh dấu hai điểm A, B trên một vòng dây không dãn có dạng đường tròn (Hình 67a), cắt cung AB của vòng dây và kéo thẳng cung đó để nhận được sợi dây như ở Hình 67b.
Đo chiều dài sợi dây đó.
Ta nói chiều dài sợi dây bằng độ dài của cung tròn AB.
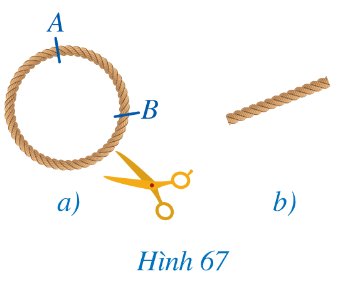
b) Ta coi mỗi đường tròn bán kính R là một cung tròn có số đo 360°. Chia đường tròn đó thành 360 phần bằng nhau, mỗi phần là cung tròn có số đo bằng 1°; chu vi của đường tròn khi đó cũng được chia thành 360 phần bằng nhau. Tính theo R:
⦁ Độ dài của cung có số đo 1°;
⦁ Độ dài của cung có số đo n°.
Thảo luận (1)Hướng dẫn giảia) Chiều dài sợi dây \(AB\) là: 5cm.
b) Độ dài cung tròn có số đo \(1^\circ \) là:
\(l = \frac{{2\pi R}}{{360}} = \frac{{\pi R}}{{180}}\).
Độ dài cung tròn có số đo \(n^\circ \) là:
\(l = \frac{{2\pi Rn}}{{360}} = \frac{{\pi Rn}}{{180}}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Một con lắc di chuyển từ vị trí A đến vị trí B (Hình 69). Tính độ dài quãng đường AB mà con lắc đó đã di chuyển, biết rằng sợi dây OA có độ dài bằng l và tia OA tạo với phương thẳng đứng góc α.
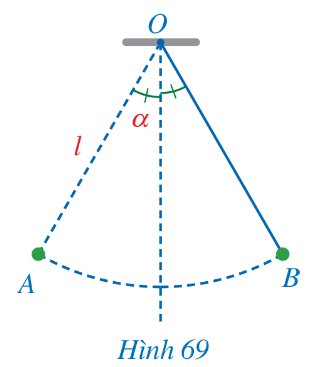
Thảo luận (1)Hướng dẫn giảiĐộ dài quãng đường \(AB\) mà con lắc đó di chuyển là:
\(AB = \frac{{\pi .l.2\alpha }}{{180}} = \frac{{\pi l\alpha }}{{90}}.\)
(Trả lời bởi Nguyễn Quốc Đạt)
Vẽ đường tròn (O; 2 cm) và các điểm A, B thỏa mãn OA < 2 cm, OB = 2 cm. Nêu nhận xét về vị trí các điểm A, B so với đường tròn (O; 2 cm).
Thảo luận (1)Hướng dẫn giải
+ Điểm \(A\) nằm trong đường tròn \(\left( {O;2cm} \right)\).
+ Điểm \(B\) nằm trên đường tròn \(\left( {O;2cm} \right)\).
(Trả lời bởi Nguyễn Quốc Đạt)
Quan sát Hình 71, hãy cho biết phần hình tròn (O) tô màu xanh được giới hạn bởi hai bán kính và cung nào?
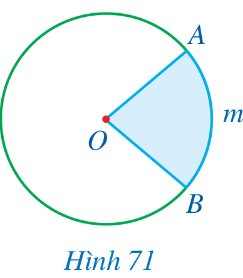
Thảo luận (1)Hướng dẫn giảiPhần hình tròn \(\left( O \right)\) tô màu xanh được giới hạn bởi hai bán kính và cung $\overset\frown{AmB}$.
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hình quạt COD giới hạn bởi hai bán kính OC, OD và cung CqD sao cho OC = CD (Hình 74). Hãy tìm số đo cung CqD ứng với hình quạt đó.
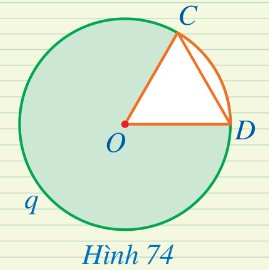
Thảo luận (1)Hướng dẫn giảiDo OC = OD nên tam giác COD là tam giác đều, suy ra \(\widehat {COD} = {60^0}\).
Vì góc COD là góc ở tâm chắn cung nhỏ CD nên sđ$\overset\frown{CD}={{60}^{o}}$.
Suy ra sđ$\overset\frown{CqD}=360^o -sđ\overset\frown{CD} = 360^o -{{60}^{o}} = 300^o$.
(Trả lời bởi Nguyễn Quốc Đạt)
Ta coi mỗi hình tròn bán kính R là một hình quạt có số đo 360°. Tính diện tích hình quạt tròn tâm O, bán kính R, biết số đo cung ứng với hình quạt tròn đó là:
a) 1°;
b) n° (Hình 75).
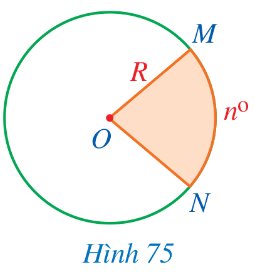
Thảo luận (1)Hướng dẫn giảia) Diện tích hình tròn là: \(S = \pi {R^2}\).
Diện tích hình quạt tròn tâm \(O\), bán kính \(R\), có số đo cung là \(1^\circ \) là: \(S = \frac{{\pi {R^2}}}{{360}}\).
b) Diện tích hình quạt tròn tâm \(O\), bán kính \(R\), có số đo cung là \(n^\circ \) là: \(S = \frac{{\pi {R^2}n}}{{360}}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Hình quạt tô màu đỏ ở Hình 65 có bán kính bằng 2 dm và góc ở tâm bằng 150°.
a) Tính diện tích của hình quạt đó.
b) Tính chiều dài cung tương ứng với hình quạt tròn đó.

Thảo luận (1)Hướng dẫn giảia) Diện tích của hình quạt đó là:
\(S = \frac{{\pi .{2^2}.150}}{{360}} \approx 5,24\left( {d{m^2}} \right)\).
b) Chiều dài cung tương ứng với hình quạt tròn đó là:
\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .2.150}}{{180}} = \frac{{5\pi }}{3}\left( {dm} \right)\).
(Trả lời bởi Nguyễn Quốc Đạt)