Nêu cách tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số. Áp dụng để tìm các đường tiệm cận của hàm số :
\(y=\dfrac{2x+3}{2-x}\)
Nêu cách tìm tiệm cận ngang và tiệm cận đứng của đồ thị hàm số. Áp dụng để tìm các đường tiệm cận của hàm số :
\(y=\dfrac{2x+3}{2-x}\)
Tìm các tiệm cận đứng và ngang của đồ thị mỗi hàm số sau :
a) \(y=\dfrac{2x-1}{x+2}\)
b) \(y=\dfrac{3-2x}{3x+1}\)
c) \(y=\dfrac{5}{2-3x}\)
d) \(y=-\dfrac{4}{x+1}\)
Thảo luận (1)Hướng dẫn giải
Tìm các tiệm cận đứng và ngang của đồ thị mỗi hàm số sau :
a) \(y=\dfrac{x^2-12x+27}{x^2-4x+5}\)
b) \(y=\dfrac{x^2-x-2}{\left(x-1\right)^2}\)
c) \(y=\dfrac{3x+\sqrt{x^2+1}}{2+\sqrt{3x^2+2}}\)
d) \(y=\dfrac{2-x}{x^2-4x+3}\)
e) \(y=\dfrac{3x+\sqrt{x^2+1}}{2+\sqrt{3x^2+2}}\)
f) \(y=\dfrac{5x-1-\sqrt{x^2-2}}{x-4}\)
Thảo luận (1)Hướng dẫn giải
a) Cho hàm số \(y=\dfrac{3-x}{x+1}\) (H)
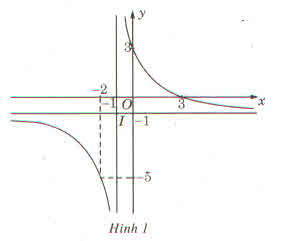
Chỉ ra một phép biến hình biến (H) thành (H') có tiệm cận ngang \(y=2\) và tiệm cận đứng \(x=2\)
b) Lấy đối xứng (H') qua gốc O, ta được hình (H"). Viết phương trình của (H")
Thảo luận (1)Hướng dẫn giảia) (H) có các đường tiệm cận là:
- Tiệm cận ngang y = -1
- Tiệm cận đứng x = -1
hai đường tiềm cận này cắt nhau tại điểm I(-1; -1).
Hình (H') có hai đường tiệm cận cắt nhau tại I'(2;2) nên ta cần phép tịnh tiến theo vector \(\overrightarrow{II'}=\left(2-\left(-1\right);2-\left(-1\right)\right)=\left(3;3\right)\)
b) Hình (H') có phương trình là:
\(y+3=\dfrac{3-\left(x+3\right)}{\left(x+3\right)+1}\) hay là \(y=\dfrac{-4x-12}{x+4}\)
Hình đối xứng với (H') qua gốc tọa độ có phương trình là:
\(-y=\dfrac{-4\left(-x\right)-12}{-x+4}\) hay là: \(y=\dfrac{4x-12}{-x+4}\)
(Trả lời bởi Giáo viên Toán)
Tìm các tiệm cận đứng và tiệm cận ngang của đồ thị hàm số:
a) \(y=\dfrac{2-x}{9-x^2}\)
b) \(y=\dfrac{x^2+x+1}{3-2x-5x^2}\)
c) \(y=\dfrac{x^2-3x+2}{x+1}\)
d) \(y=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
Thảo luận (1)Hướng dẫn giảia) Vì
và
( hoặc
và
) nên các đường thẳng: x = -3 và x = 3 là các tiệm cận đứng của đồ thị hàm số.
Vì
và
nên các đường thẳng: y = 0 là các tiệm cận ngang của đồ thị hàm số.
b) Hai tiệm cận đứng :
; tiệm cận ngang :
.
c) Tiệm cận đứng : x = -1 ;
vì
nên đồ thị hàm số không có tiệm cận ngang.
d) Hàm số xác định khi :
Vì
( hoặc
) nên đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số.
Vì
(Trả lời bởi qwerty)nên đường thẳng y = 1 là tiệm cận ngang (về bên phải) của đồ thị hàm số.
Tìm các tiệm cận của đồ thị hàm số:
a) \(y=\dfrac{x}{2-x}\)
b) \(y=\dfrac{-x+7}{x+1}\)
c) \(y=\dfrac{2x-5}{5x-2}\)
d) \(y=\dfrac{7}{x}-1\)
Thảo luận (1)Hướng dẫn giảia) Vì
( hoặc
) nên đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số.
Vì
( hoặc
) nên đường thẳng y = -1 là tiệm cận ngang của đồ thị hàm số.
b) Tiệm cận đứng : x = -1 ; tiệm cận ngang : y = -1.
c) Tiệm cận đứng :
; tiệm cận ngang :
d) Tiệm cận đứng : x = 0 ; tiệm cận ngang : y = -1.
(Trả lời bởi qwerty)