Xếp các đơn thức sau thành từng nhóm các đơn thức đồng dạng :
\(\dfrac{5}{3}x^2y\) \(xy^2\) \(-\dfrac{1}{2}x^2y\) \(-2xy^2\) \(x^2y\)
\(\dfrac{1}{4}xy^2\) \(-\dfrac{2}{5}x^2y\) \(xy\)
Tìm tổng của ba đơn thức :
\(25xy^2\) \(55xy^2\) \(75xy^2\)
Thảo luận (2)Hướng dẫn giảiTa có: \(75xy^2+25xy^2+55xy^2\)
= \(\left(75+25+55\right)xy^2\)
= \(155xy^2\)
(Trả lời bởi Ngô Quỳnh)
Tính giá trị của biểu thức sau tại x = 1 và y = -1
\(\dfrac{1}{2}x^5y-\dfrac{3}{4}x^5y+x^5y\)
Thảo luận (2)Hướng dẫn giảiTa có: \(\dfrac{1}{2}x^5y-\dfrac{3}{4}x^5y+x^5y\)
\(=\left(\dfrac{1}{2}-\dfrac{3}{4}+1\right)x^5y\)
= \(\dfrac{3}{4}x^5y\)
Thay x=1 và y=-1 vào đơn thức \(\dfrac{3}{4}x^5y\)ta được: \(\dfrac{3}{4}.1^5.\left(-1\right)\)=\(\dfrac{-3}{4}\)
(Trả lời bởi Ngô Quỳnh)
Đố :
Tên của tác giả cuốn "Đại Việt Sử kí" dưới thời vua Trần Nhân Tông được đặt cho một đường phố của Thủ đô Hà Nội. Em sẽ biết tên tác giả đó bằng cách tính các tổng và hiệu dưới đây rồi viết chữ tương ứng vào ô dưới kết quả được cho trong bảng sau :
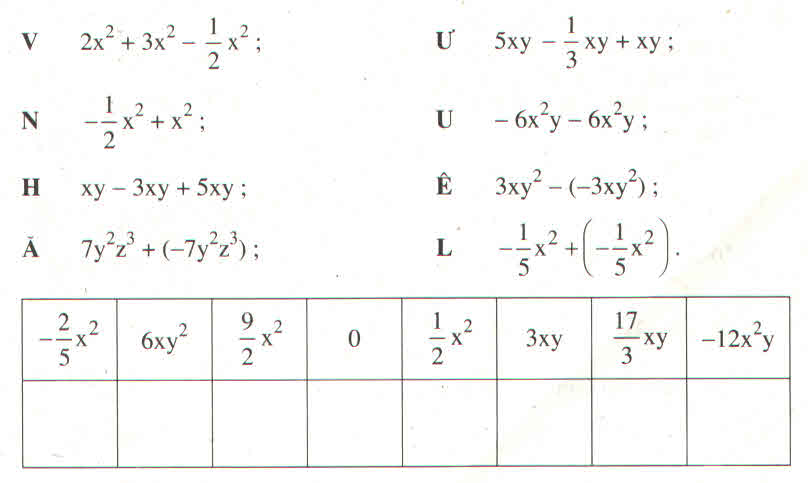
Thảo luận (3)Hướng dẫn giảiHướng dẫn giải:
Trước hết ta thu gọn các đơn thức đồng dạng để xác định mỗi chữ cái tương ứng với kết quả nào trong ô trống của bảng.
V 2x2 + 3x2 – 1212 x2 = 9292 x2;
Ư 5xy – 1313 xy + xy = 173173 xy;
N - 1212 x2 + x2 = 1212 x2;
U - 6x2y – 6x2y = -12x2y ;
H xy – 3xy + 5xy = 3xy;
Ê 3xy2 – (-3xy2) = 6 xy2;
Ă 7y2z3 + (-7y2z3) = 0;
L - 1515 x2 + (- 1515 x2) = - 2525 x2;
Vậy tên của tác giả cuốn Đại VIệt sử kí là Lê Văn Hưu.
(Trả lời bởi Thien Tu Borum)
Tính giá trị của biểu thức \(16x^2y^5-2x^3y^2\) tại \(x=0,5;y=-1\) ?
Thảo luận (3)Hướng dẫn giảiHướng dẫn giải:
Thay x = 0,5 và y = -1 vào biểu thức ta có:
16x2y5 – 2x3y2 = 16 (1212)2 (-1)5 – 2 (1212)3 (-1)2
= 16. 1414 .(-1) – 2 . 1818 . 1 = -4 - 1414 = - 174174
Vậy giá trị của biểu thức 16x2y5 – 2x3y2 tại x = 0,5 và y = -1 là - 174174
(Trả lời bởi Thien Tu Borum)
Viết ba đơn thức đồng dạng với đơn thức \(-2x^2y\) rồi tính tổng của cả bốn đơn thức đó ?
Thảo luận (1)Hướng dẫn giảiHướng dẫn giải:
Có vo số các đơn thức đồng dạng với đơn thức -2x2y. Chẳng hạn:
Ba đơn thức đồng dạng với -2x2y là:
5x2y; 23 x2y; - 13 x2y
Tổng cả bốn đơn thức:
-2x2y + 5x2y + 23 x2y + (- 13 x2y) = (-2 + 5 + 23 - 13) x2y = 103 x2y.
(Trả lời bởi Thien Tu Borum)
Tính tổng của các đơn thức :
\(\dfrac{3}{4}xyz^2\) \(\dfrac{1}{2}xyz^2\) \(-\dfrac{1}{4}xyz^2\)
Thảo luận (3)Hướng dẫn giảiTính tổng của các đơn thức: \(\dfrac{3}{4}\) xyz2; \(\dfrac{1}{2}\)xyz2; -\(\dfrac{1}{4}\)xyz2 là
\(\dfrac{3}{4}\) xyz2 + \(\dfrac{1}{2}\)xyz2 + (-\(\dfrac{1}{4}\)xyz2) = ( \(\dfrac{3}{4}+\dfrac{1}{2}-\dfrac{1}{4}\)) xyz2 = xyz2.
(Trả lời bởi Hiiiii~)
Tính tích các đơn thức sau rồi tìm bậc của đơn thức nhận được :
a) \(\dfrac{12}{15}x^4y^2\) và \(\dfrac{5}{9}xy\)
b) \(-\dfrac{1}{7}x^2y\) và \(-\dfrac{2}{5}xy^4\)
Thảo luận (2)Hướng dẫn giảiHướng dẫn giải:
a) Tích của hai đơn thức 12151215 x4y2 và 5959 xy là 12151215 x4y2 . 5959 xy = 4949 x5 y3;
Đơn thức tích có bậc 8.
b) - 1717 x2y . (-2525 xy4) = 235235 x3y5;
Đơn thức tích có bậc 8.
(Trả lời bởi Thien Tu Borum)
Điền các đơn thức thích hợp vào ô trống :
a) \(3x^2y+........=5x^2y\)
b) \(........-2x^2=-7x^2\)
c) \(.......+.......+........=x^5\)
Thảo luận (3)Hướng dẫn giảiĐiền các đơn thức thích hợp vaod chỗ trống:
a) 3x2y + □ = 5x2y → □ là 2x2y
b) □ - 2x2 = -7x2 → □ là -5 x2
c) □ + □ + □ = x5 có nhiều cách điền khác nhau:
Ba ô trống là ba đơn thức đồng dạng với và tổng 3 hệ số bằng 1 chẳng hạn 15x5 ; -12x5 ; -2x5 . Một ô là x5 , thì ô còn lại là 2 đơn thức đồng dạng có hệ đối nhau chẳng hạn: x5 ; 2x2 ; -2x2 .(Trả lời bởi Hiiiii~)
Hãy xếp các đơn thức sau thành nhóm các đơn thức đồng dạng với nhau :
\(-5x^2yz;3xy^2z;\dfrac{2}{3}x^2yz;10x^2y^2z;-\dfrac{2}{3}xy^2x;\dfrac{5}{7}x^2y^2z\)
Thảo luận (1)Hướng dẫn giảiNhóm 1:-5x\(^2\)yz;\(\dfrac{2}{3}\)x\(^2\)yz
Nhóm 2:3xy\(^2\)z;-\(\dfrac{2}{3}\)xy\(^2\)z
Nhóm 3:10x\(^2\)y\(^2\)z;\(\dfrac{5}{7}\)x\(^2\)y\(^2\)z
(Trả lời bởi Nguyên Mộng Mơ)
